数学定义

四极矩张量 Q是一个二阶张量，即一个迹（trace）为零的3x3矩阵(i.e. Qxx+Qyy+Qzz=0{\displaystyle Q_{xx}+Q_{yy}+Q_{zz}=0})。四极矩张量有9个元素，但是由于对称性和迹为零的特性，只有5个独立的元素。

对于具有相对于坐标系原点的电荷ql{\displaystyle q_{l}} 或质量 ml{\displaystyle m_{l}}和位置rl→ → -->=(rxl,ryl,rzl){\displaystyle {\vec {r_{l}}}=(r_{xl},r_{yl},r_{zl})} ）的点电荷（或在引力四极的情况下的质量）的离散系统，Q矩阵的分量由下式定义：

Qij=∑ ∑ -->lql(3rilrjl− − -->∥ ∥ -->rl→ → -->∥ ∥ -->2δ δ -->ij){\displaystyle Q_{ij}=\sum _{l}q_{l}(3r_{il}r_{jl}-\|{\vec {r_{l}}}\|^{2}\delta _{ij})}.

笛卡尔坐标x,y,z{\displaystyle x,y,z}和δ δ -->ij{\displaystyle \delta _{ij}}中的下标 i,j{\displaystyle i,j} 被称为克罗内克函数.

对于具有电荷密度（或质量密度）ρ ρ -->(x,y,z){\displaystyle \rho (x,y,z)}的连续系统，Q的分量由笛卡尔空间r上的积分来定义：

Qij=∫ ∫ -->ρ ρ -->(3rirj− − -->∥ ∥ -->r→ → -->∥ ∥ -->2δ δ -->ij)d3r{\displaystyle Q_{ij}=\int \,\rho (3r_{i}r_{j}-\|{\vec {r}}\|^{2}\delta _{ij})\,d^{3}{\mathbf {r}}}

As with any multipole moment, if a lower-order moment (monopole or dipole in this case) is non-zero, then the value of the quadrupole moment depends on the choice of the coordinate origin. For example, a dipole of two opposite-sign, same-strength point charges (which has no monopole moment) can have a nonzero quadrupole moment if the origin is shifted away from the center of the configuration (exactly between the two charges); or the quadrupole moment can be reduced to zero with the origin at the center. In contrast, if the monopole and dipole moments vanish, but the quadrupole moment does not (e.g., four same-strength charges, arranged in a square, with alternating signs), then the quadrupole moment is coordinate independent.

If each charge is the source of a "1/r{\displaystyle 1/r}" field, like the electric or gravitational field, the contribution to the field"s potential from the quadrupole moment is:

where R is a vector with origin in the system of charges and n is the unit vector in the direction of R. Here, k{\displaystyle k} is a constant that depends on the type of field, and the units being used. The factors ni,nj{\displaystyle n_{i},n_{j}} are components of the unit vector from the point of interest to the location of the quadrupole moment.

电四极

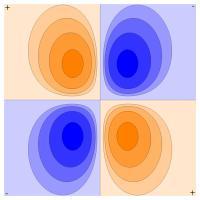
一个四极的等电势面图.

最简单的电四极情况是正方形四角上有着交变电势，但任意时刻四个电极的总电荷量为零。在此情况下，任何坐标系下的电偶极子动量都是零，但四偶极动量则不是零。此配型的电势由以下式子给出

其中 ϵ ϵ -->0{\displaystyle \epsilon _{0}} 是电容率, Qij{\displaystyle Q_{ij}} 定义同上.

推广：高阶多级器

An extreme generalization ("Point octupole") would be: Eight alternating point charges at the eight corners of a parallelepiped, e.g. of a cube with edge length a. The "octupole moment" of this arrangement would correspond, in the "octupole limit" lima→ → -->0;a3⋅ ⋅ -->Q→ → -->const.{\displaystyle \lim _{a\to 0;\,a^{3}\cdot Q\to {\rm {const.}}}}, to a nonzero diagonal tensor of order three. Still higher multipoles, e.g. of order 2, would be obtained by dipolar (quadrupolar, octupolar, ...) arrangements of point dipoles (quadrupoles, octupoles, ...), not point monopoles, of lower order, e.g. 2.

磁四极

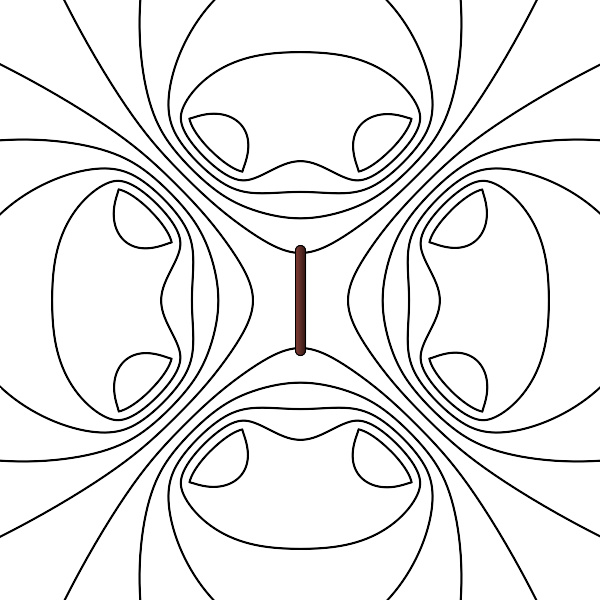
能产生四极场的线圈。

四极磁铁结构。

众所周知，磁铁分为南北两极，两极之间有磁场。然而，四极磁场将四个磁铁相互垂直放置，其中一个磁极比如南极都朝内放置，另一个磁极如北极都朝外放置，四个磁铁呈放射状。这样的结构将磁偶极矩抵消，产生一个四极矩，这样的磁场在很大范围内下降很快（相对偶极）。 An example of a magnetic quadrupole, involving permanent magnets, is depicted on the right. Electromagnets of similar conceptual design (called quadrupole magnets) are commonly used to focus beams of charged particles in particle accelerators and beam transport lines, a method known as strong focusing. The quadrupole-dipole intersect can be found by multiplying the spin of the unpaired nucleon by its parent atom. There are four steel pole tips, two opposing magnetic north poles and two opposing magnetic south poles. The steel is magnetized by a large electric current that flows in the coils of tubing wrapped around the poles.

Changing magnetic quadrupole moments produces electromagnetic radiation.

引力四极

The mass quadrupole is analogous to the electric charge quadrupole, where the charge density is simply replaced by the mass density and a negative sign is added because the masses are always positive and the force is attractive. The gravitational potential is then expressed as:

For example, because the Earth is rotating, it is oblate (flattened at the poles). This gives it a nonzero quadrupole moment. While the contribution to the Earth"s gravitational field from this quadrupole is extremely important for artificial satellites close to Earth, it is less important for the Moon, because the 1|R|3{\displaystyle {\frac {1}{|\mathbf {R} |^{3}}}} term falls quickly.

The mass quadrupole moment is also important in general relativity because, if it changes in time, it can produce gravitational radiation, similar to the electromagnetic radiation produced by oscillating electric or magnetic dipoles and higher multipoles. However, only quadrupole and higher moments can radiate gravitationally. The mass monopole represents the total mass-energy in a system, which is conserved—thus it gives off no radiation. Similarly, the mass dipole corresponds to the center of mass of a system and its first derivative represents momentum which is also a conserved quantity so the mass dipole also emits no radiation. The mass quadrupole, however, can change in time, and is the lowest-order contribution to gravitational radiation.

The simplest and most important example of a radiating system is a pair of mass points with equal masses orbiting each other on a circular orbit (an approximation to e.g. special case of binary black holes). Since the dipole moment is constant, we can for convenience place the coordinate origin right between the two points. Then the dipole moment will be zero, and if we also scale the coordinates so that the points are at unit distance from the center, in opposite direction, the system"s quadrupole moment will then simply be

where M is the mass of each point, and xi{\displaystyle x_{i}} are components of the (unit) position vector of one of the points. As they orbit, this x-vector will rotate, which means that it will have a nonzero first, and also the second time derivative (this is of course true regardless the choice of the coordinate system). Therefore the system will radiate gravitational waves. Energy lost in this way was first inferred in the changing period of the Hulse–Taylor binary pulsar, a pulsar in orbit with another neutron star of similar mass.

Just as electric charge and current multipoles contribute to the electromagnetic field, mass and mass-current multipoles contribute to the gravitational field in general relativity, causing the so-called "gravitomagnetic" effects. Changing mass-current multipoles can also give off gravitational radiation. However, contributions from the current multipoles will typically be much smaller than that of the mass quadrupole.

相关条目

多极展开

多极磁矩

固体谐波（英语：Solid harmonics）

轴向多极矩（英语：Axial multipole moments）

圆柱形多极矩（英语：Cylindrical multipole moments）

球多极矩

拉普拉斯展开

勒壤得多项式

四极离子阱

四极质谱仪

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。