定理

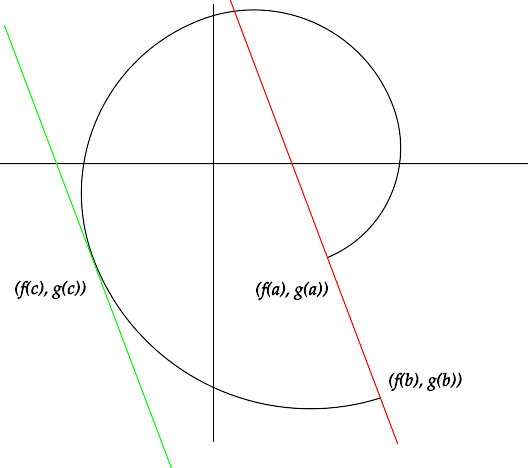
假设 I = [ a , b ] {\displaystyle I=[a,b]} 是一个实数里的闭区间，而 f : : --> I → → --> R {\displaystyle f\colon I\rightarrow \mathbb {R连续函数 是连续函数，那么其像集 f ( I ) {\displaystyle f(I)} 也是区间。它或者包含 [ f ( a ) , f ( b ) ] {\displaystyle [f(a),f(b)]} （如果 f ( a ) ≤ ≤ --> f ( b ) {\displaystyle f(a)\leq f(b)} ），或者包含 [ f ( b ) , f ( a ) ] {\displaystyle [f(b),f(a)]} （如果 f ( b ) ≤ ≤ --> f ( a ) {\displaystyle f(b)\leq f(a)} ）。换言之：

f ( I ) ⊇ ⊇ --> [ f ( a ) , f ( b ) ] {\displaystyle \displaystyle f(I)\supseteq [f(a),f(b)]} ,

或

f ( I ) ⊇ ⊇ --> [ f ( b ) , f ( a ) ] {\displaystyle \displaystyle f(I)\supseteq [f(b),f(a)]} .

介值定理通常以下述等价的形式表述：假设 f : : --> I → → --> R {\displaystyle f\colon I\rightarrow \mathbb {R} } 是连续函数，且实数 u {\displaystyle u} 满足 f ( a ) < u u > f ( b ) {\displaystyle f(a)>u>f(b)} ，则存在 c ∈ ∈ --> ( a , b ) {\displaystyle c\in (a,b)} 使得 f ( c ) = u {\displaystyle f(c)=u} 。

证明

先证明第一种情况 f ( a ) < u < f ( b ) {\displaystyle f(a) ；第二种情况也类似。

设 S {\displaystyle S} 为 [ a , b ] {\displaystyle [a,b]} 内所有 x {\displaystyle x} 的集合，使得 f ( x ) ⩽ ⩽ --> u {\displaystyle f(x)\leqslant u} 。那么 S {\displaystyle S} 是非空的，因为 a {\displaystyle a} 是 S {\displaystyle S} 的一个元素，且 S {\displaystyle S} 是上有界的，其上界为 b {\displaystyle b} 。于是，根据完备性完最小上界小上界 c = s u p {\displaystyle c=\mathrm {sup} } S {\displaystyle S} 一定存在。我们来证明 f ( c ) = u {\displaystyle f(c)=u} 。

假设 f ( c ) > u {\displaystyle f(c)>u} 。那么 f ( c ) − − --> u > 0 {\displaystyle f(c)-u>0} ，因此存在 δ δ --> > 0 {\displaystyle \delta >0} ，使得当 | x − − --> c | {\displaystyle \left|x-c\right| 时，就有 | f ( x ) − − --> f ( c ) | u {\displaystyle \left|f(x)-f(c)\right| ，因为 f {\displaystyle f} 是连续函数。但是，这样一来，当 | x − − --> c | {\displaystyle \left|x-c\right| 时，就有 f ( x ) > f ( c ) − − --> ( f ( c ) − − --> u ) = u {\displaystyle f(x)>f(c)-(f(c)-u)=u} （也就是说，对于 ( c − − --> δ δ --> , c + δ δ --> ) {\displaystyle (c-\delta ,c+\delta )} 内的 x {\displaystyle x} ，都有 f ( x ) > u {\displaystyle f(x)>u} ）。因此 c − − --> δ δ --> {\displaystyle c-\delta } 是 S {\displaystyle S} 的一个上界，与我们假设 c {\displaystyle c} 是最小上界以及 c − − --> δ δ --> < c {\displaystyle c-\delta 矛盾。

假设 f ( c ) > 0 {\displaystyle \delta >0} ，使得当 | x − − --> c | {\displaystyle \left|x-c\right| 时，就有 | f ( x ) − − --> f ( c ) | f ( c ) {\displaystyle \left|f(x)-f(c)\right| 。那么对于 ( c − − --> δ δ --> , c + δ δ --> ) {\displaystyle (c-\delta ,c+\delta )} 内的 x {\displaystyle x} ，都有 f ( x ) f ( c ) ) = u {\displaystyle f(x) ，因此存在大于 c {\displaystyle c} 的 x {\displaystyle x} ，使得 f ( x ) < u {\displaystyle f(x) ，这与 c {\displaystyle c} 的定义矛盾。

因此 f ( c ) = u {\displaystyle f(c)=u} 。

与实数完备性的关系

此定理仰赖于实数完备性，它对有理数不成立。例如函数 f ( x ) = x 2 − − --> 2 {\displaystyle f(x)=x^{2}-2} 满足 f ( 0 ) = − − --> 2 , f ( 2 ) = 2 {\displaystyle f(0)=-2,f(2)=2} ，但不存在满足 f ( x ) = 0 {\displaystyle f(x)=0} 的有理数 x {\displaystyle x} 。

零点定理（波尔查诺定理）

零点定理是介值定理的一种特殊情况－如果曲线上两点的值正负号相反，其间必定存在一个根：

由于零点定理可用来找一方程式的根，也称为 勘根定理 。伯纳德·波尔查诺于1817年证明了这个定理，同时证明了这个定理的一般情况（即介值定理）。以现代的标准来说，他的证明并不算是非常严格。

现实世界中的意义

介值定理意味着在地球的任何大圆上，温度、压强、海拔、二氧化碳的浓度（或其他任何连续变化的变量），总存在两个对跖点，在这两个点上该变量的值是相同的。

证明： 取 f 为圆上的任何连续函数。通过圆的中心作一条直线，与圆相交于点 A 和点 B 。设 d 为 f ( A ) − f ( B )的差。如果把这条直线旋转180度，将得到值− d 。根据介值定理，一定存在某个旋转角，使得 d = 0，在这个角度上便有 f ( A ) = f ( B )。

这是一个更加一般的结果——博苏克-乌拉姆定理的特殊情况。

参见

中值定理

极值定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。