解释

在物理学中，信号通常是波的形式，例如电磁波、随机振动或者声波。当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）或者谱功率分布（spectral power distribution, SPD）。功率谱密度的单位通常用每赫兹的瓦特数（W/Hz）表示，或者使用波长而不是频率，即每纳米的瓦特数（W/nm）来表示。

尽管并非一定要为信号或者它的变量赋予一定的物理量纲，下面的讨论中假设信号在时域内变化。

定义

能量谱密度

能量谱密度描述的是信号或者时间序列的能量如何随频率分布。这里，能量这个术语是用作信号处理中的推广含义； 也就是说，信号 x(t){\displaystyle x(t)} 的能量 E{\displaystyle E} 为

能量谱密度对总能量有限的瞬变信号（也就是类似于脉冲信号的）最为适用。在这种情况下，帕塞瓦尔定理给出了用傅里叶变换x^ ^ -->(f)=∫ ∫ -->− − -->∞ ∞ -->∞ ∞ -->e− − -->2π π -->iftx(t)dt{\displaystyle {\hat {x}}(f)=\int \limits _{-\infty }^{\infty }e^{-2\pi ift}x(t)dt} 表示信号能量的形式。

这里频率 f{\displaystyle f} 单位为Hz，即每秒周期数。经常使用角频率ω ω -->=2π π -->f{\displaystyle \omega =2\pi f}。由于右边的积分是信号的能量，被积函数 |x^ ^ -->(f)|2{\displaystyle |{\hat {x}}(f)|^{2}} 可以理解为频率为 f{\displaystyle f} 的信号中单位频率包含的能量的密度函数。鉴于此，信号 x(t){\displaystyle x(t)} 的能量谱密度定义为

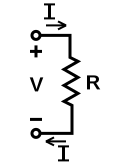
举一个物理上的例子来说明如何测量信号的能量谱密度，假设 V(t){\displaystyle V(t)} 表示阻抗为 Z{\displaystyle Z} 的传输线上传播的电脉冲的电势（单位伏特），并假设传输线末端是一个匹配电阻器（因而所有脉冲能量都传到电阻器上并且不会反射回来）。由欧姆定律，t{\displaystyle t} 时刻传递到电阻器的功率等于 V(t)2/Z{\displaystyle V(t)^{2}/Z}，因此总能量可以通过以时间为变量对 V(t)2/Z{\displaystyle V(t)^{2}/Z} 积分。要求得频率 f{\displaystyle f} 时的能量谱密度 Sxx(f){\displaystyle S_{xx}(f)}，可以在传输线和电阻器之间加入一个只允许感兴趣的频率附近的很窄频率范围（Δ Δ -->f{\displaystyle \Delta f}）通过的带通滤波器，并测量电阻器上消耗的总能量 E(f){\displaystyle E(f)}。f{\displaystyle f} 处的能量谱密度的值为 E(f)/Δ Δ -->f{\displaystyle E(f)/\Delta f}。在此例子中，由于功率 V(t)2/Z{\displaystyle V(t)^{2}/Z} 的单位为 V Ω，能量 E(f){\displaystyle E(f)} 的单位是 V s Ω = J，因此能量谱密度 E(f)/Δ Δ -->f{\displaystyle E(f)/\Delta f} 的单位为 J Hz。在许多情况下，常常不去除以 Z{\displaystyle Z}，于是单位就会是 V s Hz。

这个定义直接地推广到了有无穷个值的离散信号 xn{\displaystyle x_{n}}，比如一个离散时间采样的信号 xn=x(nΔ Δ -->t){\displaystyle x_{n}=x(n\,\Delta t)}：

其中 x^ ^ -->d(f){\displaystyle {\hat {x}}_{d}(f)} 是 xn{\displaystyle x_{n}} 的离散傅里叶变换，而 x^ ^ -->d∗ ∗ -->(f){\displaystyle {\hat {x}}_{d}^{*}(f)} 是 x^ ^ -->d(f){\displaystyle {\hat {x}}_{d}(f)} 的复共轭。采样区间 Δ Δ -->t{\displaystyle \Delta t} 需要保持正确的物理单位并确保我们能恢复极限情况下 Δ Δ -->t→ → -->0{\displaystyle \Delta t\rightarrow 0} 连续的情况；不过在数学中往往将此区间设为1。

功率谱密度

上面能量谱密度的定义适用于能量集中在一个时间窗口附近的瞬变（脉冲状信号）；因此信号的傅里叶变换一般存在。对于持续存在的连续信号，如平稳过程，就必须定义功率谱密度（PSD）；这描述了一个信号或时间序列的功率随频率的分布，正如前面给出的简单例子一样。在这里，功率可以是实际的物理功率，不过更多时候，为了更方便用于抽象信号，简单地确定为信号的平方值。例如，统计学系研究时间（或其他独立变量）的函数 x(t) 的方差，并类比电信号，习惯称之为功率谱，即使没有涉及到物理上的功率。若要创建一个 x(t) 的物理电压源并加在1欧姆的电阻器两端，于是在电阻器上消耗的瞬时功率就会是 x瓦特。

下面的时间平均给出了信号 x(t){\displaystyle x(t)} 的平均功率 P：

注意平稳过程有可能功率有限但能量无限。毕竟，能量是功率的积分，而平稳信号持续无限长时间。这就是在这些情况下不能使用上面定义的能量谱密度的原因。

在分析信号 x(t){\displaystyle x(t)} 的频率内容时，可能会计算傅里叶变换 x^ ^ -->(ω ω -->){\displaystyle {\hat {x}}(\omega )}；但许多感兴趣的信号的傅里叶变换都不存在。 由于这种复杂性，可以用仅仅在有限区间 [0, T] 把信号积分的截短傅里叶变换 x^ ^ -->T(ω ω -->){\displaystyle {\hat {x}}_{T}(\omega )}：

因此功率谱密度可以被定义为

这里 E 表示期望值；明确地，我们有

在后面形式中（对一个平稳随机过程来说），可以改换变量 Δ Δ -->t=t− − -->t′{\displaystyle \Delta t=t-t"}，随着积分的极限（而非 [0,T]）趋近于无穷，所得信号的功率谱密度 Sxx(ω ω -->){\displaystyle S_{xx}(\omega )} 与自相关函数可视为傅里叶变换对（维纳－辛钦定理）。自相关函数是一个定义为 γ γ -->(τ τ -->)=⟨ ⟨ -->X(t)X(t+τ τ -->)⟩ ⟩ -->{\displaystyle \gamma (\tau )=\langle X(t)X(t+\tau )\rangle } 的统计量（或更一般地，在 X(t) 是复值函数时为 γ γ -->(τ τ -->)=⟨ ⟨ -->X(t)X∗ ∗ -->(t+τ τ -->)⟩ ⟩ -->{\displaystyle \gamma (\tau )=\langle X(t)X^{*}(t+\tau )\rangle }）。倘若 γ γ -->(τ τ -->){\displaystyle \gamma (\tau )} 是绝对可积的（并不总是如此），

许多作者实际上用这个等式来定义功率谱密度。

给定频带 [f1,f2]{\displaystyle [f_{1},f_{2}]}（或[ω ω -->1,ω ω -->2]{\displaystyle [\omega _{1},\omega _{2}]}）中信号的功率可以通过对频率积分计算。由于 Sxx(− − -->ω ω -->)=Sxx(ω ω -->){\displaystyle S_{xx}(-\omega )=S_{xx}(\omega )}，正、负频率的功率相同，因而下面形式中的因子为2（这种因子取决于使用的惯例）：

更一般地，类似的技术可以被用来估计一个随时间变化的光谱密度。更一般地，可以使用类似的方法来估计时变谱密度。在这种情况下上面定义的 (0, T) 上的截短傅里叶变换不是通过 T 趋近于无穷的极限计算的。这导致光谱覆盖率和分辨率降低，因为不会采样小于 1/T 的频率，而 1/T 的整数倍频率的结果不是独立的。

性质

f(t){\displaystyle f(t)} 的谱密度和 f(t){\displaystyle f(t)} 的自相关组成一个傅里叶变换对（对于功率谱密度和能量谱密度来说，使用着不同的自相关函数定义）。

通常使用傅里叶变换技术估计谱密度，但是也可以使用如Welch法（Welch"s method）和最大熵这样的技术。

傅里叶分析的结果之一就是Parseval定理（Parseval"s theorem），这个定理表明能量谱密度曲线下的面积等于信号幅度平方下的面积，总的能量是：

：上面的定理在离散情况下也是成立的。另外的一个结论是功率谱密度下总的功率与对应的总的平均信号功率相等，它是逐渐趋近于零的自相关函数。

相关概念

大多数“频率”图实际上仅仅表示了谱密度。有时完整的频率要用两部分来表示，一部分是对应于频率的“幅度”（它就是谱密度），另外一部分是对应于频率的“相位”（它包含了频谱中剩余的其它信息）。信号 f(t) 可以从一个完整的频谱进行恢复。需要注意的是 f(t) 不能仅仅从谱密度这一部分进行恢复——它丢失了“临时信息”。

信号的 谱矩心（spectral centroid） 是谱密度函数的中点，也就是说将整个分布切分成两个相等部分的点。

谱密度是频率的函数，而不是时间的函数。但是，也可以计算一个较长信号上一小段“窗口”的谱密度，并且根据与事件相关的窗口进行绘图，这样的图形称为频谱图（spectrogram)。这是短时傅里叶变换和小波等许多谱分析技术的基础。

应用

电子工程

信号功率谱的概念和应用是电子工程的基础，尤其是在电子通信系统中，例如无线电和微波通信、雷达以及相关系统。人们已经花费了很大的精力和大量的金钱投入到开发、生产“频谱分析仪”这种电子设备，用来帮助电子工程师、技术人员、技工观察、测量电子信号的功率谱。频谱分析仪的价格根据带宽和精度的不同而不同，质量最好的仪器的价格超过 100，000 美元。

色度学

光源的频谱是每个频率携带的功率或者光源中“颜色”的度量。光谱通常是沿着可见光在波长空间而不是频率空间测量的不同点（通常是 31 个点）进行测量，它不是严格意义上的谱密度。一些分光光度计能够分辨高达 1 到 2纳米的增量精度，测量值用来计算其它的规格然后绘制出来显示光源的频谱属性。这对于分析特定光源的颜色特性来说是一个非常有用的工具。

参见

噪声的颜色

谱泄漏

窗函数

频域

频谱

双谱

^Oppenheim; Verghese. Signals, Systems, and Inference. : 32–4. 

^2.02.1Stein, Jonathan Y. Digital Signal Processing: A Computer Science Perspective. Wiley. 2000: 115. 

^Hannes Risken.The Fokker–Planck Equation: Methods of Solution and Applications2nd. Springer. 1996: 30. ISBN 9783540615309. 

^Fred Rieke; William Bialek & David Warland. Spikes: Exploring the Neural Code (Computational Neuroscience). MIT Press. 1999. ISBN 978-0262681087. 

^5.05.1Scott Millers & Donald Childers. Probability and random processes. Academic Press. 2012: 370–5. 

^TheWiener–Khinchin theoremmakes sense of this formula for anywide-sense stationary processunder weaker hypotheses: γ γ -->{\displaystyle \gamma } does not need to be absolutely integrable, it only needs to exist. But the integral can no longer be interpreted as usual. The formula also makes sense if interpreted as involvingdistributions(in the sense ofLaurent Schwartz, not in the sense of a statisticalCumulative distribution function) instead of functions. If γ γ -->{\displaystyle \gamma } is continuous, Bochner"s theorem can be used to prove that its Fourier transform exists as a positivemeasure, whose distribution function is F (but not necessarily as a function and not necessarily possessing a probability density).

^Dennis Ward Ricker.Echo Signal Processing. Springer. 2003. ISBN 1-4020-7395-X. 

引用错误：页面中存在标签，但没有找到相应的标签

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。