定义

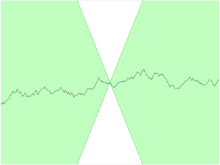
对于利普希茨连续函数，存在一个双圆锥(白色)其顶点可以沿着曲线平移，使得曲线总是完全在这两个圆锥外。

对于在实数集的子集的函数f: : -->D⊆ ⊆ -->R→ → -->R{\displaystyle f\colon D\subseteq \mathbb {R} \to \mathbb {常数 } ，若存在常数K{\displaystyle K}，使得|f(a)− − -->f(b)|≤ ≤ -->K|a− − -->b|∀ ∀ -->a,b∈ ∈ -->D{\displaystyle |f(a)-f(b)|\leq K|a-b|\quad \forall a,b\in D}，则称f{\displaystyle f} 符合利普希茨条件，对于f{\displaystyle f} 最小的常数K{\displaystyle K} 称为 f{\displaystyle f} 的利普希茨常数。

若K<1{\displaystyle K<1}，f{\displaystyle f} 称为收缩映射。

利普希茨条件也可对任意度量空间的函数定义：

给定两个度量空间(M,dM),(N,dN){\displaystyle (M,d_{M}),(N,d_{N})}，U⊆ ⊆ -->M{\displaystyle U\subseteq M}。若对于函数f:U→ → -->N{\displaystyle f:U\to N}，存在常数K{\displaystyle K} 使得

则说它符合利普希茨条件。

若存在K≥ ≥ -->1{\displaystyle K\geq 1}使得

则称f{\displaystyle f}为双李普希茨(bi-Lipschitz)的。

皮卡-林德洛夫定理

若已知y(t){\displaystyle y(t)}有界，f{\displaystyle f}符合利普希茨条件，则微分方程初值问题y′(t)=f(t,y(t)),y(t0)=y0{\displaystyle y"(t)=f(t,y(t)),\quad y(t_{0})=y_{0}}刚好有一个解。

在应用上，t{\displaystyle t}通常属于一有界闭区间（如[0,2π π -->]{\displaystyle [0,2\pi ]}）。于是y(t){\displaystyle y(t)}必有界，故y{\displaystyle y}有唯一解。

例子

f:[− − -->3,7]→ → -->R,f(x)=x2{\displaystyle f:[-3,7]\to \mathbb {R} ,\quad f(x)=x^{2}}符合利普希茨条件，K=14{\displaystyle K=14}。

f:R→ → -->R,f(x)=x2{\displaystyle f:\mathbb {R} \to \mathbb {R} ,\quad f(x)=x^{2}}不符合利普希茨条件，当x→ → -->∞ ∞ -->,f′(x)→ → -->∞ ∞ -->{\displaystyle x\to \infty ,\quad f"(x)\to \infty }。

定义在所有实数值的f(x)=x2+5{\displaystyle f(x)={\sqrt {x^{2}+5}}}符合利普希茨条件，K=1{\displaystyle K=1}。

f(x)=|x|{\displaystyle f(x)=|x|}符合利普希茨条件，K=1{\displaystyle K=1}。由此可见符合利普希茨条件的函数未必可微。

f:[0,1]→ → -->[0,1],f(x)=x{\displaystyle f:[0,1]\to [0,1],\quad f(x)={\sqrt {x}}}不符合利普希茨条件，x→ → -->0,f′(x)→ → -->∞ ∞ -->{\displaystyle x\to 0,\quad f"(x)\to \infty }。不过，它符合赫尔德条件。

当且仅当处处可微函数f的一次导函数有界，f符利普希茨条件。这是中值定理的结果。所有C1{\displaystyle C^{1}}函数都是局部利普希茨的，因为局部紧致空间的连续函数必定有界。

性质

符合利普希茨条件的函数一致连续，也连续。

bi-Lipschitz函数是单射的。

Rademacher定理：若A⊆ ⊆ -->Rn{\displaystyle A\subseteq \mathbb {R} ^{n}}且A{\displaystyle A}为开集，f:A″→ → -->Rn{\displaystyle f:A""\to \mathbb {R} ^{n}}符利普希茨条件，则f几乎处处可微。

Kirszbraun定理：给定两个希尔伯特空间H1,H2{\displaystyle H_{1},H_{2}}，U∈ ∈ -->H1{\displaystyle U\in H_{1}}，f:U→ → -->H1{\displaystyle f:U\to H_{1}}符合利普希茨条件，则存在符合利普希茨条件的F:H1→ → -->H2{\displaystyle F:H_{1}\to H_{2}}，使得F{\displaystyle F}的利普希茨常数和f{\displaystyle f}的相同，且F(x)=f(x)∀ ∀ -->x∈ ∈ -->U{\displaystyle F(x)=f(x)\quad \forall x\in U}。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。