历史

1940年，汉明于贝尔实验室（Bell Labs）工作，运用贝尔模型V（Bell Model V）电脑，一个周期时间在几秒钟内的机电继电器机器。输入端是依靠打孔卡（Punched Card），这不免有些读取错误。在平日，特殊代码将发现错误并闪灯（flash lights），使得操作者能够纠正这个错误。在周末和下班期间，在没有操作者的情况下，机器只会简单地转移到下一个工作。

汉明在周末工作，他对于不可靠的读卡机发生错误后，总是必须重新开始专案变得愈来愈沮丧。在接下来的几年中，他为了解决侦错的问题，开发了功能日益强大的侦错算法。在1950年，他发表了今日所称的汉明码。现在汉明码有着广泛的应用。

汉明码之前

人们在汉明码出现之前使用过多种检查错误的编码方式，但是没有一个可以在和汉明码在相同空间消耗的情况下，得到相等的效果。

奇偶

奇偶校验是一种添加一个奇偶位用来指示之前的数据中包含有奇数还是偶数个1的检验方式。如果在传输的过程中，有奇数个位发生了改变，那么这个错误将被检测出来（注意奇偶位本身也可能改变）。一般来说，如果数据中包含有奇数个1的话，则将奇偶位设定为1；反之，如果数据中有偶数个1的话，则将奇偶位设定为0。换句话说，原始数据和奇偶位组成的新数据中，将总共包含偶数个1.

奇偶校验并不总是有效，如果数据中有偶数个位发生变化，则奇偶位仍将是正确的，因此不能检测出错误。而且，即使奇偶校验检测出了错误，它也不能指出哪一位出现了错误，从而难以进行更正。数据必须整体丢弃并且重新传输。在一个噪音较大的媒介中，成功传输数据可能需要很长时间甚至不可能完成。虽然奇偶校验的效果不佳，但是由于他只需要一位额外的空间开销，因此这是开销最小的检测方式。并且，如果知道了发生错误的位，奇偶校验还可以恢复数据。

汉明码

如果一条信息中包含更多用于纠错的位，且通过妥善安排这些纠错位使得不同的出错位产生不同的错误结果，那么我们就可以找出出错位了。在一个7位的信息中，单个位出错有7种可能，因此3个错误控制位就足以确定是否出错及哪一位出错了。

汉明研究了包括五取二码在内的编码方案，并归纳了他们的想法。

通用算法

下列通用算法可以为任意位数字产生一个可以纠错一位（英语：Single Error Correcting）的汉明码。

从1开始给数字的数据位（从左向右）标上序号, 1，2，3，4，5...

将这些数据位的位置序号转换为二进制，1, 10, 11, 100, 101,等。

数据位的位置序号中所有为二的幂次方的位（编号1，2，4，8，等，即数据位位置序号的二进制表示中只有一个1）是校验位

所有其它位置的数据位（数据位位置序号的二进制表示中至少2个是1）是数据位

每一位的数据包含在特定的两个或两个以上的校验位中，这些校验位取决于这些数据位的位置数值的二进制表示

采用奇校验还是偶校验都是可行的。偶校验从数学的角度看更简单一些，但在实践中并没有区别。

校验位一般的规律可以如下表示：

观察上表可发现一个比较直观的规律：第i个检验位是第2位，从该位开始，检验2位，跳过2位……依次类推。例如上表中第3个检验位p4从第2=4位开始，检验4、5、6、7共4位，然后跳过8、9、10、11共4位，再检验12、13、14、15共4位……

例子

对11000010进行汉明编码，求编码后的码字。

1.列出表格，从左往右（或从右往左）填入数字，但2的次方的位置不填。

2.把数据行有1的列的位置写为二进制。

3.收集所有二进制数字，求异或。0011⊕ ⊕ -->0101⊕ ⊕ -->1011=1101{\displaystyle 0011\oplus 0101\oplus 1011=1101}

4.把1101依次填入表格中2的次方的位置（低位在左）。

5.所以编码后的码字是101110010010。

带附加奇偶校验码的汉明码（SECDED）

(7,4)汉明码

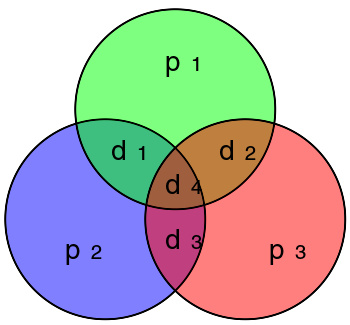
Graphical depiction of the 4 data bits and 3 parity bits and which parity bits apply to which data bits

1950年，汉明介绍了(7,4)代码。其编码由4资料比特到7位，增加三个奇偶校验码。(7,4)汉明码可以检测并纠正单比特差错，且也能检测双比特差错。

建立奇偶检验矩阵

矩阵G:=(Ik|− − -->AT){\displaystyle \mathbf {G} :={\begin{pmatrix}I_{k}|-A^{T}\\\end{pmatrix}}}被称为（标准）生成矩阵线性(n,k)码。

和H:=(A|In− − -->k){\displaystyle \mathbf {H} :={\begin{pmatrix}A|I_{n-k}\\\end{pmatrix}}}奇偶检验矩阵验矩阵。

编码

范例

从上述矩阵我们有2=2=16码词。

二进制码x→ → -->{\displaystyle {\overrightarrow {x}}}的码词可以从x→ → -->=a→ → -->G{\displaystyle {\overrightarrow {x}}={\overrightarrow {a}}G}得到。对a→ → -->=a1a2a3a4{\displaystyle {\overrightarrow {a}}=a_{1}a_{2}a_{3}a_{4}}和ai{\displaystyle a_{i}}存在F2{\displaystyle F_{2}}(一个只有0和1的二元域）。

故此码表即是所有4个三元组（k个三元组）。

因而，（1,0,1,1）编码为（0,1,1,0,0,1,1）。

(8,4)汉明码

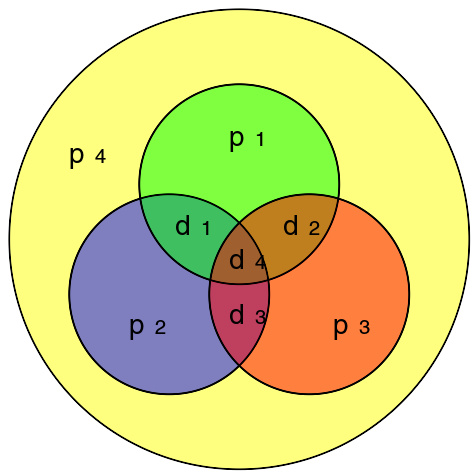
The same (7,4) example from above with an extra parity bit

(7,4)汉明码可以很容易地编码为一个(8,4)码，通过在(7,4)编码词（参见(7,4)汉明码）上附加一个额外的奇偶位。

这可以用下面修正的矩阵相加：

和

注意，H{\displaystyle \mathbf {H} }并非用标准形式表示。为了得到G{\displaystyle \mathbf {G} }，原子行操作能够被用来获得一个等价的矩阵对陈形式的H{\displaystyle \mathbf {H} }：

(11,7)汉明码

相关条目

格雷码

汉明距离

前向纠错

里德-所罗门码

参考文献

Moon, Todd K.Error Correction Coding. New Jersey: John Wiley & Sons. 2005. ISBN 978-0-471-64800-0. 

MacKay, David J.C.Information Theory, Inference and Learning Algorithms.Cambridge: Cambridge University Press. 2003-09. ISBN 0-521-64298-1. 

D.K. Bhattacharryya, S. Nandi. An efficient class of SEC-DED-AUED codes. 1997 International Symposium on Parallel Architectures, Algorithms and Networks（ISPAN "97）: 410–415. doi:10.1109/ISPAN.1997.645128. 

^See Lemma 12 of

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。