性质

平行六面体可由正方体经线性变换而成。

用相同的平行六面体，可以镶嵌整个空间。

体积

基本公式

平行六面体的体积是底面 A{\displaystyle A} 与高 h{\displaystyle h} 的乘积，即

这里的高是底面与对面的垂直距离。

以向量计算

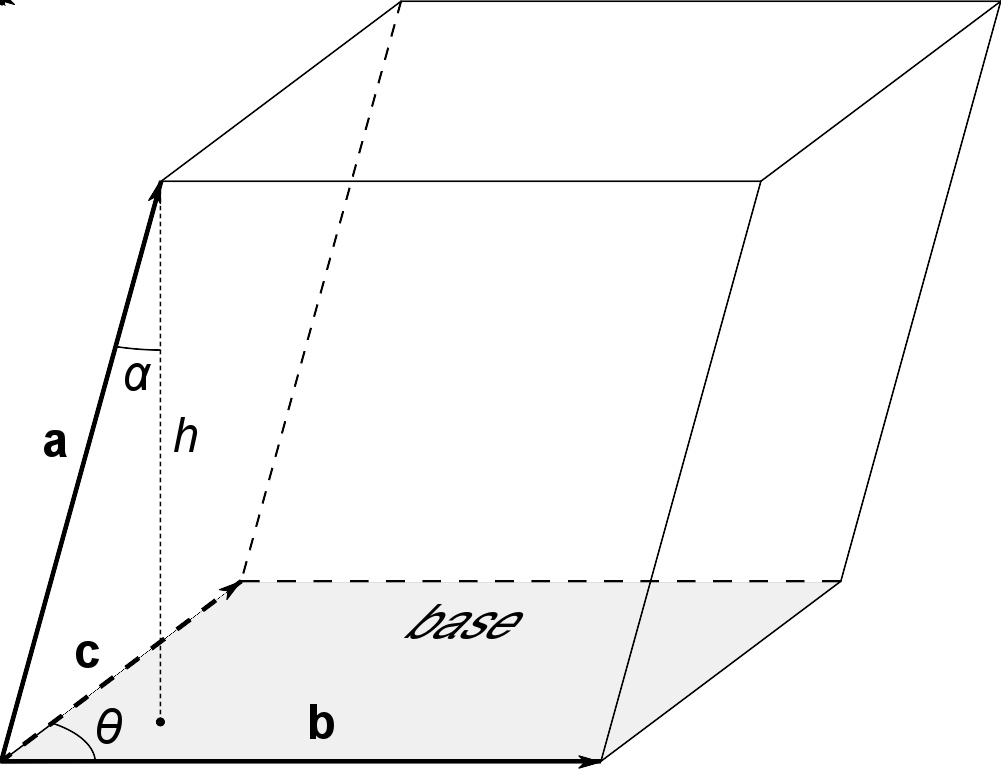
用向量来定义平行六面体。

另外一个方法是用向量 a=(a1,a2,a3){\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3})} ， b=(b1,b2,b3){\displaystyle \mathbf {b} =(b_{1},b_{2},b_{3})} ，以及 c=(c1,c2,c3){\displaystyle \mathbf {c} =(c_{1},c_{2},c_{3})} 来表示相交于一点的三条棱。平行六面体的体积 V{\displaystyle V} 等于标量三重积：

证明：

以 b{\displaystyle \mathbf {b} } 和 c{\displaystyle \mathbf {c} } 来表示底面的边，则根据向量积的定义，底面的面积 A{\displaystyle A} 为：

其中 θ θ -->{\displaystyle \theta } 是 b{\displaystyle \mathbf {b} } 与 c{\displaystyle \mathbf {c} } 之间的角，而高为：

其中 α α -->{\displaystyle \alpha } 是 a{\displaystyle \mathbf {a} } 与 h{\displaystyle h} 之间的角。

从图中我们可以看到， α α -->{\displaystyle \alpha } 的大小限定为 0∘ ∘ -->≤ ≤ -->α α -->{\displaystyle 0^{\circ }\leq \alpha c{\displaystyle \mathbf {b} \times \mathbf {c} } 与 a{\displaystyle \mathbf {a} } 之间的角 β β -->{\displaystyle \beta } 则有可能大于90°（0∘ ∘ -->≤ ≤ -->β β -->{\displaystyle 0^{\circ }\leq \beta c{\displaystyle \mathbf {b} \times \mathbf {c} } 与 h{\displaystyle h} 平行， β β -->{\displaystyle \beta } 的值要么等于 α α -->{\displaystyle \alpha } ，要么等于 180∘ ∘ -->− − -->α α -->{\displaystyle 180^{\circ }-\alpha } 。因此：

且

我们得出结论：

于是，根据标量积的定义，它等于 a⋅ ⋅ -->(b× × -->c){\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )} 的绝对值，即：

证毕。

最后一个表达式也可以写成以下行列式的绝对值：

以棱长及夹角计算

若 a{\displaystyle a} 、b{\displaystyle b} 及 c{\displaystyle c} 是三条两两相邻的棱长，且α α -->{\displaystyle \alpha } 、 β β -->{\displaystyle \beta } 及 γ γ -->{\displaystyle \gamma } 是三条棱边的夹角，则平行六面体的体积为：

证明

从上面可知，平行六面体的体积可表示为：

其中：

因此

依行列式及标量积定义展开公式右手边，即可得上述公式。

以座标计算

选取任意一顶点 (x1,y1,z1){\displaystyle (x_{1},y_{1},z_{1})} 以其相邻三个顶点 (x2,y2,z2){\displaystyle (x_{2},y_{2},z_{2})} 、 (x3,y3,z3){\displaystyle (x_{3},y_{3},z_{3})} 及 (x4,y4,z4){\displaystyle (x_{4},y_{4},z_{4})} ，则体积可表示为：

参考文献

Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 122, 1973.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。