几何性质

正五胞体作为一个单纯形，是自身对偶的。当它穿过三维空间时其截体积最大时，其截体是一个半正的正三棱柱。它的二胞角度数是cos (1/4)，约等于75.52°。对于一个边长为a的正五胞体，其超体积是 5 a 4 96 {\displaystyle {\cfrac {{\sqrt {5}}a^{4}}{96}}} ,表体积是 5 2 a 3 12 {\displaystyle {\cfrac {5{\sqrt {2}}a^{3}}{12}}} 。

若一个正五胞体的棱长为1，则其外接超球的半径为 10 5 ≈ ≈ --> 0.632455532 {\displaystyle {\frac {\sqrt {10}}{5}}\approx 0.632455532} ,外中交超球(经过正五胞体各棱中点的三维超球)半径为 15 10 ≈ ≈ --> 0.3872983346 {\displaystyle {\frac {\sqrt {15}}{10}}\approx 0.3872983346} ，内中交超球(经过正五胞体各面中心的三维超球)半径为 15 15 ≈ ≈ --> 0.2581988897 {\displaystyle {\frac {\sqrt {15}}{15}}\approx 0.2581988897} ，内切超球半径为 10 20 ≈ ≈ --> 0.158113883 {\displaystyle {\frac {\sqrt {10}}{20}}\approx 0.158113883} 。

顶点坐标

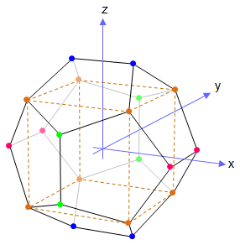
对于一个边长为2，中心在四维直角坐标系原点上的正五胞体，它的5个顶点坐标分别是

如果把正五胞体作为一个五维直角坐标系中的四维平面，则它的顶点坐标会简单得多，为(0,0,0,0,1)或(0,1,1,1,1)的全排列（其中正五胞体棱长为 2 {\displaystyle {\sqrt {2}}} ），分别对应五维正轴形（正三十二超胞体）或五维半正方体。

对称群结构

正五胞体属于四维单纯形，它有着A 4 对称结构，对应施莱夫利符号{3,3,3}，考斯特符号 ，该群的群阶为120。

可视化

相关多胞体和堆砌

正五胞体是由考克斯特群[3,3,3]构造出来的9个半正多胞体中最简单的一个。

参考

Regular Convex Four-Dimensional Polytopesby David Fontaine,提供了部分关于正五胞体的几何数据。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。