列表

在 列表 中，数据项的顺序是确定的，也可以存在多个相同的数据项。列表支持的操作包括查找项目并找到其位置（若存在），将项目从列表中删除，在特定位置插入项目等。通常的队列，或称FIFO即是一个列表，该列表只能在一端添加项目，而在另一端删除项目。而栈，或LIFO则只能在同一端添加或删除项目。不管是队列还是栈，集合中项目的顺序都应当是一定的，因此这两种情况只是列表的特例。其它列表支持的操作包括排序，再一次说明了其中顺序的重要性。

列表的具体形式包括数组，链表等。

集

与列表不同，在 集 中，数据项是无序的，也不允许存在相同数据项。集支持添加、删除和查找项目。一些语言内建对集的支持，而在其它语言中，可以利用散列表实现集。

多重集

多重集 的行为类似于集，其中数据项是无序的。但在多重集中，可以存在相同的数据项。多重集支持的操作包括添加、删除项，查询相同项在多重集现的次数。多重集可以通过排序转换成列表。

关联数组

关联数组 （或称 查找表 ， 字典 等）的行为和字典相似，为 键 （例如字典中的单词）输入提供一个 值 （如字典中的定义）输出。 值 可以是对复杂数据结构的引用。通常使用散列表实现高效率的关联数组。

树

二叉树是树的一种类型

在 树 中，“根”节点与一定数量的数据项以亲-子关系联系起来，而其子数据项也与另外的数据项以同样的方式联系。除了根节点的每个项都有且只有一个父节点，并可能有一些子节点。树支持的操作包括遍历，插入等。用于排序操作的树通常称为堆。通常使用树来保存存在包含亲-子关系的数据，例如菜单，目录及其中文件等。

图

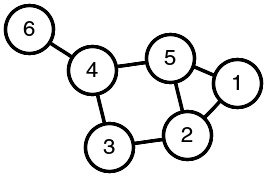
一张6节点图

在 图 中，每个数据项都可以与一个或多个其它数据项联系起来，其中每个节点都是平等的，类似于无根节点、无亲-子关系的树。图支持的操作包括遍历，查找等。图常常用于对实际问题进行建模，并解决这些问题。在生成树协议中，建立一张代表网络结构的图（或称网格），从而了解应当断开哪些链路以避免数据回圈。

抽象概念及其实现

如上所述，集合，以及集合的各种分类都只是抽象概念。由于名字相同或相似，集合及其在各种语言中的实现常常会造成文字上的混淆。集合，列表，集，树等名字究竟是数据结构，抽象数据类型抑或类只能通过具体分析来确定。其中，集合则是计算问题的解决方案中抽象程度最高的概念。从这个方面来看，若过于关注其实现，则可能会对理解集合的数学概念产生反作用。

参见

数据结构

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。