证明

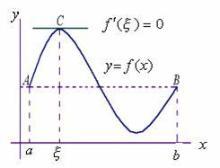
罗尔定理的几何意义

首先，因为f{\displaystyle f}在闭区间[a,b]{\displaystyle [a,b]}上连续，根据极值定理，f{\displaystyle f}在[a,b]{\displaystyle [a,b]}上有最大值和最小值。如果最大值和最小值都在端点a{\displaystyle a}或b{\displaystyle b}处取得，由于f(a)=f(b){\displaystyle f(a)=f(b)}，f{\displaystyle f}显然是一个常数函数。那么对于任一点ξ ξ -->∈ ∈ -->(a,b){\displaystyle \xi \in (a,b)}，我们都有f′ ′ -->(ξ ξ -->)=0{\displaystyle f^{\prime }(\xi )=0}。

现在假设f{\displaystyle f}在ξ ξ -->∈ ∈ -->(a,b){\displaystyle \xi \in (a,b)}处取得最大值。我们只需证明f{\displaystyle f}在该点导数为零。

取x∈ ∈ -->(a,ξ ξ -->){\displaystyle x\in (a,\xi )}，由最大值定义f(ξ ξ -->)≥ ≥ -->f(x){\displaystyle f(\xi )\geq f(x)}，那么f(x)− − -->f(ξ ξ -->)x− − -->ξ ξ -->≥ ≥ -->0{\displaystyle {\frac {f(x)-f(\xi )}{x-\xi }}\geq 0}。令x→ → -->ξ ξ -->− − -->{\displaystyle x\rightarrow \xi ^{-}}，则limx→ → -->ξ ξ -->− − -->f(x)− − -->f(ξ ξ -->)x− − -->ξ ξ -->≥ ≥ -->0{\displaystyle \lim _{x\rightarrow \xi ^{-}}{\frac {f(x)-f(\xi )}{x-\xi }}\geq 0}。因为f{\displaystyle f}在ξ ξ -->{\displaystyle \xi }处可导，所以我们有f′(ξ ξ -->)≥ ≥ -->0{\displaystyle f"(\xi )\geq 0}。

取x∈ ∈ -->(ξ ξ -->,b){\displaystyle x\in (\xi ,b)}，那么f(x)− − -->f(ξ ξ -->)x− − -->ξ ξ -->≤ ≤ -->0{\displaystyle {\frac {f(x)-f(\xi )}{x-\xi }}\leq 0}。这时令x→ → -->ξ ξ -->+{\displaystyle x\rightarrow \xi ^{+}}，则有limx→ → -->ξ ξ -->+f(x)− − -->f(ξ ξ -->)x− − -->ξ ξ -->≤ ≤ -->0{\displaystyle \lim _{x\rightarrow \xi ^{+}}{\frac {f(x)-f(\xi )}{x-\xi }}\leq 0}，所以f′(ξ ξ -->)≤ ≤ -->0{\displaystyle f"(\xi )\leq 0}。

于是，f′(ξ ξ -->)=0{\displaystyle f"(\xi )=0}。

f{\displaystyle f}在ξ ξ -->∈ ∈ -->(a,b){\displaystyle \xi \in (a,b)}处取得最小值的情况同理。

例子

第一个例子

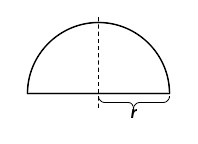
半径为r的半圆

考虑函数

（其中r > 0。）它的图像是中心位于原点的半圆。这个函数在闭区间[−r,r]内连续，在开区间(−r,r)内可导（但在终点−r和r处不可导）。由于f(−r) = f(r)，因此根据罗尔定理，存在一个导数为零的点。

第二个例子

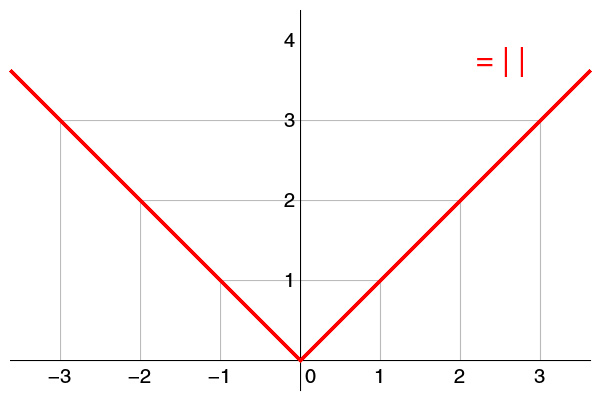
绝对值函数的图像

如果函数在区间内的某个点不可导，则罗尔定理的结论不一定成立。对于某个a > 0绝对值绝对值函数：

那么f(−a) = f(a)，但−a和a之间不存在导数为零的点。这是因为，函数虽然是连续的，但它在点x = 0不可导。注意f的导数在x = 0从-1变为1，但不取得值0。

推广形式

第二个例子表明罗尔定理下面的一般形式：

考虑一个实值，在闭区间[a,b]上的连续函数，并满足f(a) = f(b).如果对开区间(a,b)内的任意x，右极限

而左极限

在扩展的实数轴[−∞,∞]上存在，那么开区间(a,b)内就存在c使得这两个极限

f′(c+){\displaystyle f"(c+)\quad }和f′(c− − -->){\displaystyle \quad f"(c-)}

中其中一个≥ 0，另一个≤ 0（在扩展的实数轴上）。如果对任何x左极限和右极限都相同，那么它们对c也相等，于是在c处f的导函数存在且等于零。

参见

中值定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。