例子

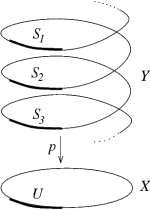
覆叠空间的例子：R→ → -->S1{\displaystyle \mathbb {R} \to \mathbb {S} ^{1}}

考虑映射p:R→ → -->S1{\displaystyle p:\mathbb {R} \to \mathbb {S} ^{1}}，p(x)=e2π π -->ix{\displaystyle p(x)=e^{2\pi ix}}。对任意s=e2π π -->it∈ ∈ -->S1{\displaystyle s=e^{2\pi it}\in \mathbb {S} ^{1}}，取其开邻域

由此可见p:R→ → -->S1{\displaystyle p:\mathbb {R} \to \mathbb {S} ^{1}}是覆叠映射。

莫比乌斯带的二重复叠空间是 S1× × -->[0,1]{\displaystyle \mathbb {S} ^{1}\times [0,1]}。

性质

局部性质 对于任何一个覆叠p:C→ → -->X{\displaystyle p:C\to X}都是一个局部同胚，这就是说，对任意的c \in C，都存在一个在C中的开邻域U，和p(c)在X中的开邻域V，使得p在U上的限制诱导U到V上的同胚。这说明C和X在局部上的拓扑性质是一样的。如果X是单连通的且C是连通的，则在整体上也成立，并且覆叠p变为同胚。 纤维上的同胚

万有覆叠空间

连通空间X{\displaystyle X}的万有覆叠空间（若其存在）是范畴CovX{\displaystyle \mathbf {Cov} _{X}}的初始对象u:X~ ~ -->→ → -->X{\displaystyle u:{\tilde {X}}\to X}，换言之，对每个覆叠p:X′→ → -->X{\displaystyle p:X"\to X}，存在唯一的连续映射f:X~ ~ -->→ → -->X′{\displaystyle f:{\tilde {X}}\to X"}使得p∘ ∘ -->f=u{\displaystyle p\circ f=u}。万有覆叠若存在则必唯一。之前的R→ → -->S1{\displaystyle \mathbb {R} \to \mathbb {S} ^{1}}便是一例。

若要求X{\displaystyle X}局部道路连通且局部单连通，则万有覆叠空间存在。这类空间的主要例子有流形和单纯复形。在同样前提下，覆叠X~ ~ -->→ → -->X{\displaystyle {\tilde {X}}\to X}是万有覆叠基本群条件是基本群π π -->1(X~ ~ -->,∗ ∗ -->)={e}{\displaystyle \pi _{1}({\tilde {X}},*)=\{e\}}。

正则覆叠及主丛

以下同样要求X{\displaystyle X}连通、局部道路连通且局部单连通。对于覆叠映射p:Y→ → -->X{\displaystyle p:Y\to X}，选定x∈ ∈ -->X{\displaystyle x\in X}。在CovX{\displaystyle \mathbf {Cov} _{X}}中的自同构群Aut(p){\displaystyle \mathrm {Aut} (p)}在纤维p− − -->1(x){\displaystyle p^{-1}自由)}上的作用是自由的（即：Aut(p)→ → -->Aut(p− − -->1(x)){\displaystyle \mathrm {Aut} (p)\to \mathrm {Aut} (p^{-1}(x))}是单射），对于x∈ ∈ -->X{\displaystyle x\in X}的不同选取，此作用仅差个自然的同构。

若Aut(p){\displaystyle \mathrm {Aut} (p)}的作用是传递的，则称p:Y→ → -->X{\displaystyle p:Y\to X}为正则覆叠。万有覆叠必正则，反之则不然。按照纤维丛的观点，覆叠空间正是离散纤维的纤维丛，正则覆叠对应到主丛。

文献

Hatcher, Allen.Algebraic Topology. Cambridge University Press. 2002. ISBN 0-521-79540-0. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。