生物学上的意义

以下将式子乘开，如此可以较容易地解释方程式的实际意义。

猎物族群的增值速度

第一式所表达的是猎物族群的增值速度：

此模型假设猎物所接受的食物供给已经达到最极限，且除非遭遇掠食者的捕食，否则繁殖数量的增加以指数方式成长，其指数成长的情形，则以上述方程式中的 αx 表现。此外并假设猎物遭遇捕食的比例，和猎物遭遇掠食者的机会成常数比，以上述方程式中的 βxy 表现。如果 x 或 y 其中一个为零，则皆有可能是没有捕食行为出现。

由上述的方程式可知：猎物族群规模的改变，源于本身受到捕食而产生的成长衰减。

掠食者族群的增值速度

第二式所表达的是掠食者族群的增值速度：

此方程式中的 δxy 表示掠食者族群的成长（可能会与掠食者与猎物的数量比例相似，但是掠食者与猎物的数量比例是以不同的常数表示，且不一定与族群的成长相等。） γy 表示掠食者的自然死亡，为指数衰减。

由上述的方程式可知：掠食者族群规模的改变，是猎食者族群的成长，减去其自然死亡的部分。

方程式的解

此方程式拥有周期性的解，但没有解析解。通过龙格－库塔法的数字计算之后，掠食者与猎物的族群大可以表达成两个曲线图形。生态上的实际大致依照此简单模式，不过详细状况会有所出入。

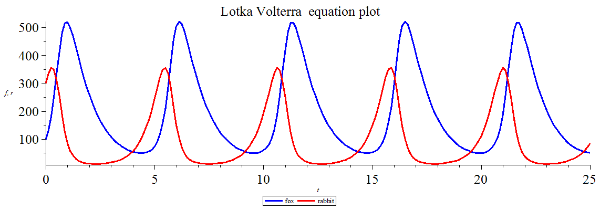
洛特卡－沃尔泰拉方程

在此模式系统中，当猎物数量充足的时候，掠食者的族群也会兴旺起来。不过掠食者的族群最后仍然会因为超过猎物所能供给的数量而开始衰减。当掠食者的族群族群缩减，则猎物族群将会再次增大。两者的族群大以周期性的成长与衰减进行循环。

族群规模的平衡

族群的平衡会发生在族群大小不再变化的时候。例如：两条微分方程皆等于零的时候。

求解上述方程式的 x 与 y 可得：

以及

由此可知有两组解。

第一组解实际上是表示两个物种的灭绝，若是两个族群皆为零，则此状况将永久持续下去。第二组解表示一个不动点，意思是两个族群能够维持一个不为零的数量，并且在简单的模型中能够永久持续。系数 α, β, γ, 与 δ ，能够决定族群规模将在哪种情况下达成平衡状态。

不动点的稳定性

不动点的稳定性可以利用偏导数，将其以线性化方式呈现。

产生的掠食者猎物模型之雅可比矩阵如下：

第一不动点

当数值为(0,0)稳定状态，则雅可比矩阵变成：

此矩阵的特征值为：

模型中的 α 与 γ 永远比零大，且每一的特征值的符号永远不一样。由此可知位在原点的不动点是一个鞍点（saddle point）。

此不动点的稳定性相当重要，当处于稳定态的时候，非零的族群会趋向它。一些初始的族群可能会走向灭绝。然而当不动点位于原点时，也是一个鞍点，因此并不稳定。所以在此模型中，两个物种皆难以灭绝。除非以人为方式将猎物完全消灭，并使掠食者因饥荒而死亡。而若是将掠食者完全消灭，则猎物的族群增长情形，将会脱离此简单模型。

第二不动点

在第二不动点求 J 值可得：

此矩阵的特征值为：

当特征值皆为复数时，此不动点为一个焦点。实部为零使其成为一个中心。 这表示掠食者与猎物族群规模呈现循环消长，并且以此不动点为中心来回震荡。

饱和沃尔泰拉方程

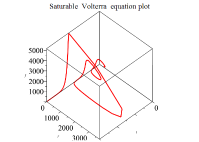
饱和沃尔泰拉方程 3d 图

饱和沃尔泰拉方程

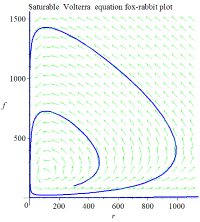
饱和沃尔泰拉方程 xy 图

d r d t = 2 ∗ ∗ --> r ( t ) − − --> α α --> ∗ ∗ --> r ( t ) ∗ ∗ --> f ( t ) 1 + s ∗ ∗ --> r ( t ) {\displaystyle {\frac {dr}{dt}}=2*r(t)-{\frac {\alpha *r(t)*f(t)}{1+s*r(t)}}} ;

d f d t = − − --> f ( t ) + α α --> ∗ ∗ --> r ( t ) ∗ ∗ --> f ( t ) 1 + s ∗ ∗ --> r ( t ) {\displaystyle {\frac {df}{dt}}=-f(t)+{\frac {\alpha *r(t)*f(t)}{1+s*r(t)}}}

图示当 α=0.01，s=0.001 时的饱和沃尔泰拉方程。

著名例子

加拿大的山猫（Lynx）与雪兔（Snowshoe Hare）数量消长情形。

参见

洛特卡－沃尔泰拉种间竞争方程

群体动力学

生物数学

参考文献

E. R. Leigh (1968) The ecological role of Volterra"s equations, in Some Mathematical Problems in Biology - a modern discussion using Hudson"s Bay Company data on lynx and hares in Canada from 1847 to 1903.

Understanding Nonlinear Dynamics. Daniel Kaplan and Leon Glass.

Vito Volterra. Variations and fluctuations of the number of individuals in animal species living together. In Animal Ecology . McGraw-Hill, 1931. Translated from 1928 edition by R. N. Chapman.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。