



欧拉﹣伯努力栋梁方程
历史普遍认为,伽利略是提出关于梁的重要理论的第一人,但是近代史家发现,达芬奇才是第一位研究梁的科学家。但是由于当时缺乏建材弹性的研究和数学基础(主要是微积分),导致伽利略等的科学家没有成功取得突破。1750年,瑞士学者莱昂哈德·欧拉(LeonhardEuler)与丹尼尔·伯努利(DanielBernoulli)开始研究梁并把梁理论推向实用,成功地把科学与工程学区分成两个学科,同时使得工程学成为了一门数理科学。欧拉-伯努力梁方程欧拉─伯努利梁方程内容描述了梁的位移与载重的关系:而其中:u{\displaystyle\textstyle{u}\,}为位移∂∂-->u∂∂-->x{\displaystyle\textstyle{\frac{\partialu}{\partialx}}\,}为梁的斜率,−−-->EI∂∂-->2u∂∂-->x2{\displaystyle\textstyle{-E...
历史
普遍认为,伽利略是提出关于梁的重要理论的第一人,但是近代史家发现,达芬奇才是第一位研究梁的科学家。但是由于当时缺乏建材弹性的研究和数学基础(主要是微积分),导致伽利略等的科学家没有成功取得突破。1750年,瑞士学者莱昂哈德·欧拉(Leonhard Euler)与丹尼尔·伯努利(Daniel Bernoulli)开始研究梁并把梁理论推向实用,成功地把科学与工程学区分成两个学科,同时使得工程学成为了一门数理科学。
欧拉-伯努力梁方程
欧拉─伯努利梁方程内容描述了梁的位移与载重的关系:
而其中:
u{\displaystyle \textstyle {u}\,} 为位移
∂ ∂ -->u∂ ∂ -->x{\displaystyle \textstyle {\frac {\partial u}{\partial x}}\,} 为梁的斜率,
− − -->EI∂ ∂ -->2u∂ ∂ -->x2{\displaystyle \textstyle {-EI{\frac {\partial ^{2}u}{\partial x^{2}}}}\,} 为梁的弯矩,
− − -->∂ ∂ -->∂ ∂ -->x(EI∂ ∂ -->2u∂ ∂ -->x2){\displaystyle \textstyle {-{\frac {\partial }{\partial x}}\left(EI{\frac {\partial ^{2}u}{\partial x^{2}}}\right)}\,} 是梁的剪力。
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 欧拉方程
历史第一份印有欧拉方程的出版物是欧拉的论文《流体运动的一般原理》(Principesgénérauxdumouvementdesfluides),发表于1757年,刊载于《柏林科学院论文集》(Mémoiresdel"AcademiedesSciencesdeBerlin)。它们是最早被写下来的一批偏微分方程。在欧拉发表他的研究之时,方程组只有动量方程及连续性方程,因此只能完整描述非压缩性流体;在描述可压缩性流体时,会因条件不足而不能提供唯一解。在1816年,皮埃尔-西蒙·拉普拉斯添加了一条方程,第三条方程后来被称为绝热条件。在十九世纪的后半期,科学家们发现,与能量守恒相关的方程在任何时间都得被遵守,而绝热条件则只会在有平滑解的情况下会被遵守,因为该条件是由平滑解时的基础定律所造成的后果。在发现了狭义相对论之后,能量密度、质量...
· 欧拉-拉格朗日方程
第一方程设f=f(x,y,z){\displaystylef=f(x,\y,\z)},以及fy,fz{\displaystylef_{y},\f_{z}}在[a,b]××-->R2{\displaystyle[a,\b]\times\mathbb{R}^{2}}中连续,并设泛函若y∈∈-->C1[a,b]{\displaystyley\inC^{1}[a,\b]}使得泛函J(y){\displaystyleJ(y)}取得局部平稳值,则对于所有的x∈∈-->(a,b){\displaystylex\in(a,\b)},推广到多维的情况,记若y→→-->′(x)∈∈-->(C1[a,b])n{\displaystyle{\vec{y}}"(x)\in(C^{1}[a,b])^{n}}使得泛函J(y→→-->)=∫∫-->...
· 欧拉公式
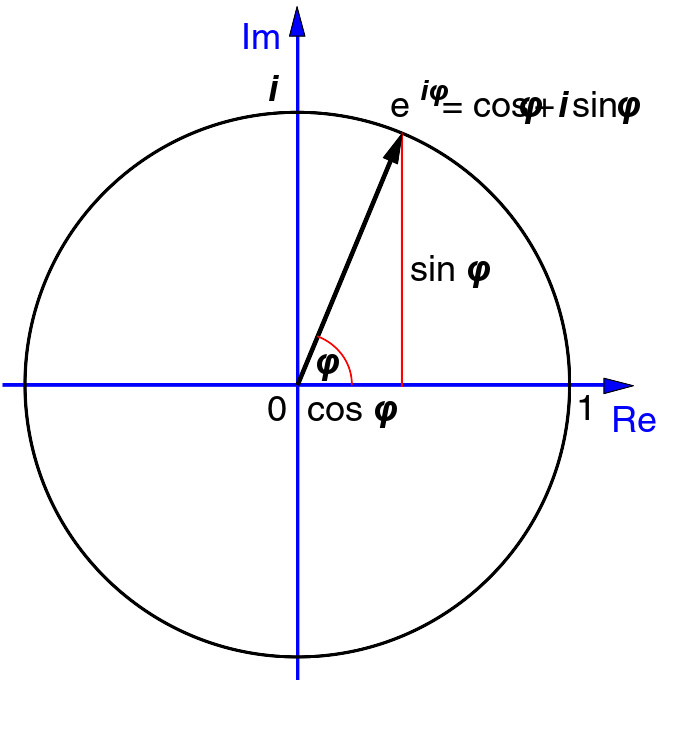
形式对于任意实数x{\displaystylex\,},以下恒真:由此也可以推导出sin-->x=eix−−-->e−−-->ix2i{\displaystyle\sinx={\frac{e^{ix}-e^{-ix}}{2i}}}及cos-->x=eix+e−−-->ix2{\displaystyle\cosx={\frac{e^{ix}+e^{-ix}}{2}}}。当x=ππ-->{\displa欧拉tylex=\pi\,}时,欧拉公式的特殊形式为eiππ-->+1=0{\displaystyle欧拉恒等式\pi}+1=0\,}。(参见欧拉恒等式)cis函数在复分析领域,欧拉公式亦可以以函数的形式表示并且一般定义域为θθ-->∈∈-->R{\displaystyle\theta\in\mathbb{R}\,},值域为θθ--&...
· 伯拉纠
参见伯拉纠主义参考书目甘乃迪(JohnW.Kennedy)。《见证的火炬-二千年教会的属灵历史》。刘志雄译。桃园:提比哩亚,1997。比尔‧奥斯汀(BillR.Austin)。《基督教发展史》。马杰伟等译。香港:种籽,1991。奥尔森(RogerE.Olson)。《神学的故事》。吴瑞诚、徐成德译。台北:校园,2002。谢家树。《基督教历代别异神学思想简介》。台北:中国主日学协会,1983。谭国才。《教会历史上课讲义》。台北:基督教台湾浸会神学院,2012。毕尔麦尔(Bihlmeyer)等。《古代教会史》。雷立柏(L.Leeb)译。北京:宗教文化出版社,2009。
· 欧拉乘积
定义假设a{\displaystylea}为一积性函数,则狄利克雷级数等于欧拉乘积其中,乘积对所有素数p{\displaystylep}进行,P(p,s){\displaystyleP(p,s)}则可表示为这可以看作形式母函数,形式欧拉乘积展开的存在性与a(n){\displaystylea(n)}为积性函数两者互为充要条件。a(n){\displaystylea(n)}为完全积性函数时可得到一重要的特例。此时P(p,s){\displaystyleP(p,s)}为等比级数,有当a(n)=1{\displaystylea(n)=1}时即为黎曼ζ函数,更一般的情形则是狄利克雷特征。参考文献G.Polya,InductionandAnalogyinMathematicsVolume1PrincetonUniversityPress(1954)L.C.Card53-6388(Averyacces...
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信















