定理

设空间闭区域Ω是由分片光滑的闭曲面Σ所围起来的三维区域，函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数，则有

或

这里Σ是Ω的边界（boundary），cos α、cos β、cos γ是Σ在点(x,y,z)处的单位法向量的方向余弦。

这两个公式都叫做高斯公式，不过这两公式仅仅是表达方式不同，其实是相同的定理，这可以用变数变换得到两公式的右边都等于 ∫ ∫ -->Σ Σ -->(P,Q,R)⋅ ⋅ -->ndS{\displaystyle \int _{\Sigma }(P,Q,R)\cdot \mathbf {n} \,dS}，其中 n{\displaystyle \mathbf {n} } 是曲面 Σ Σ -->{\displaystyle \Sigma } 的向外单位法向量。

用散度表示

高斯公式用散度表示为：

其中Σ是空间闭区域Ω的边界曲面，而 n{\displaystyle \mathbf {n} } 是曲面Σ上的朝外的单位法向量。

用向量表示

令V代表有一间单闭曲面S为边界的体积，f{\displaystyle \mathbf {f} }是定义在V中和S上连续可微的向量场。如果dS{\displaystyle d\mathbf {S} }是外法向向量面元，则

推论

对于标量函数g和向量场F的积，应用高斯公式可得：

对于两个向量场F× × -->G{\displaystyle \mathbf {F} \times \mathbf {G} }的向量积，应用高斯公式可得：

对于标量函数f和非零常向量的积，应用高斯公式可得：

对于向量场F和非零常向量的向量积，应用高斯公式可得：

例子

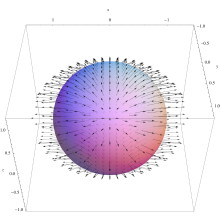
例子所对应的向量场。注意，向量可能指向球面的内侧或者外侧。

假设我们想要计算

其中S是一个单位球面，定义为

F是向量场

直接计算这个积分是相当困难的，但我们可以用高斯公式来把它简化：

其中W是单位球:

由于函数y和z是奇函数，我们有：

因此：

因为单位球W的体积是4π/3.

二阶张量的高斯公式

二阶张量的高斯公式实际上是上面的高斯公式的推论。为了使内容完整，首先简要地介绍三维欧几里得空间上的二阶张量（详见并矢张量或张量积）以及相关的概念和记号。在这里，向量和向量场用黑斜体字母表示，张量用正黑体字母表示。

两个向量a{\displaystyle {\boldsymbol {a}}}和b{\displaystyle {\boldsymbol {b}}}并排放在一起所形成的量ab{\displaystyle {\boldsymbol {ab}}}被称为向量a{\displaystyle {\boldsymbol {a}}}和b{\displaystyle {\boldsymbol {b}}}的并矢或并矢张量。要注意，一般来说，ab≠ ≠ -->ba{\displaystyle {\boldsymbol {ab}}\neq {\boldsymbol {ba}}}。

ab=0{\displaystyle {\boldsymbol {ab}}=0}的充分必要条件是a=0{\displaystyle {\boldsymbol {a}}=0}或b=0{\displaystyle {\boldsymbol {b}}=0}。

二阶张量就是有限个并矢的线性组合。

ab{\displaystyle {\boldsymbol {ab}}}分别线性地依赖于a{\displaystyle {\boldsymbol {a}}}和b{\displaystyle {\boldsymbol {b}}}。

二阶张量T{\displaystyle \mathbf {T} }和向量a{\displaystyle {\boldsymbol {a}}}的缩并T⋅ ⋅ -->a{\displaystyle \mathbf {T} \cdot {\boldsymbol {a}}}以及a⋅ ⋅ -->T{\displaystyle {\boldsymbol {a}}\cdot \mathbf {T} }对 T{\displaystyle \mathbf {T} }和a{\displaystyle {\boldsymbol {a}}}都是线性的。

特别是，当T=uv{\displaystyle \mathbf {T} ={\boldsymbol {uv}}}时，

所以，一般说来，T⋅ ⋅ -->a≠ ≠ -->a⋅ ⋅ -->T{\displaystyle \mathbf {T} \cdot {\boldsymbol {a}}\neq {\boldsymbol {a}}\cdot \mathbf {T} }。

下面举一个例子：用二阶张量及其与向量的缩并来重新写(a× × -->b)× × -->c{\displaystyle ({\boldsymbol {a}}\times {\boldsymbol {b}})\times {\boldsymbol {c}}}和a× × -->(b× × -->c){\displaystyle {\boldsymbol {a}}\times ({\boldsymbol {b}}\times {\boldsymbol {c}})}。

我们还用到二阶张量T{\displaystyle \mathbf {T} }的转置T′{\displaystyle \mathbf {T} "}（又可以记为Tt{\displaystyle \mathbf {T} ^{\mathrm {t} }}），定义如下：

T′{\displaystyle \mathbf {T} "}仍然是一个二阶张量，并且线性地依赖于T{\displaystyle \mathbf {T} }。

(uv)′=vu{\displaystyle ({\boldsymbol {uv}})"={\boldsymbol {vu}}}。

定理：设 V{\displaystyle V}是三维欧几里得空间中的一个有限区域，S{\displaystyle S}是它的边界曲面，n^ ^ -->{\displaystyle {\hat {\boldsymbol {n}}}}是S{\displaystyle S法线外法线方单位向量位向量，T{\displaystyle \mathbf {T} }是定义在V{\displaystyle V}的某个开邻域上的C1{\displaystyle C^{1}}连续的二阶张量场，T′{\displaystyle \mathbf {T} "}是T{\displaystyle \mathbf {T} }的转置，则

证明：下面以第二个式子为例进行证明。令第二个式子的左边为F{\displaystyle {\boldsymbol {F}}}，则

接下来利用向量场的高斯公式，可得

于是

至此证毕。

参阅

格林定理

斯托克斯定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。