定义

设 V{\displaystyle V} 为有限维实向量空间，并赋予标准的内积(,){\displaystyle (,)}。V{\displaystyle V} 中的根系是有限个向量（称为根）构成的集合 Φ Φ -->{\displaystyle \Phi }，满足下述条件：

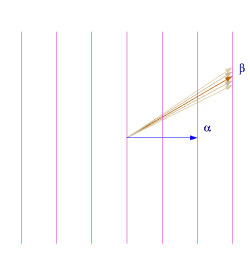
的整性条件使得 β 必然落在所示各条垂直线上。再配合 的整性条件，在每条线上，其间交角只有两种可能。

Φ Φ -->{\displaystyle \Phi } 的元素张出 V{\displaystyle V}。

对任一 α α -->∈ ∈ -->Φ Φ -->{\displaystyle \alpha \in \Phi }，其属于 Φ Φ -->{\displaystyle \Phi } 的标量倍数只有 ± ± -->α α -->{\displaystyle \pm \alpha }。

对任意 α α -->∈ ∈ -->Φ Φ -->{\displaystyle \alpha \in \Phi }，集合 Φ Φ -->{\displaystyle \Phi } 在对 α α -->{\displaystyle \alpha } 的反射之下不变。在此的反射是指 σ σ -->α α -->(β β -->)=β β -->− − -->2(α α -->,β β -->)(α α -->,α α -->)α α -->∈ ∈ -->Φ Φ -->.{\displaystyle \sigma _{\alpha }(\beta )=\beta -2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\alpha \in \Phi .}

（整性）若 α α -->,β β -->∈ ∈ -->Φ Φ -->{\displaystyle \alpha ,\beta \in \Phi }，则 β β -->{\displaystyle \beta } 在 α α -->{\displaystyle \alpha } 方向的投影乘以2是 α α -->{\displaystyle \alpha } 的整数倍，即： ⟨ ⟨ -->β β -->,α α -->⟩ ⟩ -->:=2(α α -->,β β -->)(α α -->,α α -->)∈ ∈ -->Z,{\displaystyle \langle \beta ,\alpha \rangle :=2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\in \mathbb {Z} ,}

根据性质三，整性等价于：对任意 α α -->,β β -->∈ ∈ -->Φ Φ -->{\displaystyle \alpha ,\beta \in \Phi }，σ σ -->α α -->(β β -->){\displaystyle \sigma _{\alpha }(\beta )} 与 β β -->{\displaystyle \beta } 仅差 α α -->{\displaystyle \alpha } 的整数倍。此外，注意到性质四定义的尖积

并非一个内积，它未必对称，而且只对第一个参数是线性的。

根系 Φ Φ -->{\displaystyle \Phi } 的秩定义为 V{\displaystyle V} 的维度。

给定两个根系 (V,Φ Φ -->),(W,Ψ Ψ -->){\displaystyle (V,\Phi ),(W,\Psi )}，可考虑其正交直和 V⊕ ⊕ -->W{\displaystyle V\oplus W}，则 Φ Φ -->⊔ ⊔ -->Ψ Ψ -->{\displaystyle \Phi \sqcup \Psi } 自然地构成其中的根系。若一个根系无法表成如此的组合（当然，假设 V,W≠ ≠ -->{0}{\displaystyle V,W\neq \{0\}}），则称之为不可约的。

对两个根系 (E1,Φ Φ -->1),(E2,Φ Φ -->2){\displaystyle (E_{1},\Phi _{1}),(E_{2},\Phi _{2})}，若存在其间的线性同构，使得 Φ Φ -->1{\displaystyle \Phi _{1}} 映至 Φ Φ -->2{\displaystyle \Phi _{2}}，则称它们为同构的根系。

对于根系 (V,Φ Φ -->){\displaystyle (V,\Phi )}，对根的反射生成一个群，称为该根系的外尔群。可证明此群在 Φ Φ -->{\displaystyle \Phi } 上忠实地作用，因此必为有限群。

秩一与秩二的例子

在同构的意义下，秩一的根系仅有一种，由两个非零向量 ± ± -->α α -->{\displaystyle \pm \alpha } 组成。此根系记作 A1{\displaystyle A_{1}}。

秩二的根系有四种，图解如下：

当 Φ Φ -->{\displaystyle \Phi } 是 V{\displaystyle V} 中的根系，而 W{\displaystyle W} 是 Ψ Ψ -->=Φ Φ -->∩ ∩ -->W{\displaystyle \Psi =\Phi \cap W} 在 W{\displaystyle W} 中生成的子空间，则 Ψ Ψ -->{\displaystyle \Psi } 是 W{\displaystyle W} 中的根系。因此上述列表限制了任意秩根系中两根的几何关系，例如：任意两根的交角仅可能是 0,30,45,60,90,120,135,150{\displaystyle 0,30,45,60,90,120,135,150} 或 180{\displaystyle 180} 度。

正根与单根

对于根系 Φ Φ -->{\displaystyle \Phi }，可以取定满足下述条件的正根子集 Φ Φ -->+{\displaystyle \Phi ^{+}}：

对每个根 α α -->∈ ∈ -->Φ Φ -->{\displaystyle \alpha \in \Phi }，α α -->,− − -->α α -->{\displaystyle \alpha ,-\alpha } 中恰有一者属于 Φ Φ -->+{\displaystyle \Phi ^{+}}。

对任意 α α -->,β β -->∈ ∈ -->Φ Φ -->+{\displaystyle \alpha ,\beta \in \Phi ^{+}}，若 α α -->+β β -->∈ ∈ -->Φ Φ -->{\displaystyle \alpha +\beta \in \Phi }，则 α α -->+β β -->∈ ∈ -->Φ Φ -->+{\displaystyle \alpha +\beta \in \Phi ^{+}}。

正根的取法并不唯一。取定一组正根后，− − -->Φ Φ -->+{\displaystyle -\Phi ^{+}} 的元素被称为负根。

正根的选取等价于单根的选取。单根集是 Φ Φ -->{\displaystyle \Phi } 中满足下述条件的子集 Δ Δ -->{\displaystyle \Delta }：

选定一组单根后，可定义相应的正根为展开式中系数大于等于零的根。如此可得到单根与正根选取法的一一对应。

以邓肯图分类根系

不可约根系与某类被称为邓肯图的图间有一一对应关系。邓肯图的分类是简单的组合学问题，由此可导出不可约根系的分类定理。其构造方式如下：

给定一个不可约根系，选取一组单根。相应的邓肯图以这些单根为顶点。两个单根 α α -->,β β -->{\displaystyle \alpha ,\beta } 若不垂直，则有 ⟨ ⟨ -->α α -->,β β -->⟩ ⟩ -->⋅ ⋅ -->⟨ ⟨ -->β β -->,α α -->⟩ ⟩ -->{\displaystyle \langle \alpha ,\beta \rangle \cdot \langle \beta ,\alpha \rangle } 个边相连：若只有一个边，则不取定向，否则则取自长度 (α α -->,α α -->){\displaystyle (\alpha ,\alpha )} 长者（称为长根）指向短者（称为短根）的有向边。

一个根系可以取多种不同的单根。然而，由于外尔群在这些选取上的作用是传递的，邓肯图的构造与单根的选取无关，它是根系内在的不变量。反之，给定具有相同邓肯图的两个不可约根系，可以按图配对单根及其间的内积，从而得到根系的同构。邓肯图给出的内积未必唯一，但至多差一个正常数倍，因而得到的根系是同构的 。

借此，可将不可约根系的分类问题化约到连通邓肯图的分类。若某个邓肯图来自于根系，则从其顶点与边定义的双线性形式必然是邓肯的；配上这个条件后，即可解决根系的分类。

邓肯图的分类列表详如下图。下标表示图中的顶点数，亦即相应根系的秩。

不可约根系的性质

不可约根系依其邓肯图的种类命名。有四族根系：An,Bn,Cn,Dn{\displaystyle A_{n},B_{n},C_{n},D_{n}}，其下标分别取遍 n≥ ≥ -->1,2,3,4{\displaystyle n\geq 1,2,3,4} 的正整数，称为典型根系；剩下五种情形称为例外根系。下标表示根系之秩。在上表中， |Φ Φ --><|{\displaystyle |\Phi ^{ 表示短根的个数（若诸根同长，则皆视为长根），I{\displaystyle I} 表示其嘉当矩阵的行列式，而 |W|{\displaystyle |W|} 表示外尔群之阶。

不可约根系的构造方法及描述

An

取 V{\displaystyle V} 为 Rn+1{\displaystyle \mathbb {R} ^{n+1}} 中满足 ∑ ∑ -->i=1nxi=0{\displaystyle \sum _{i=1}^{n}x_{i}=0} 的点 (x1,… … -->,xn){\displaystyle (x_{1},\ldots ,x_{n})} 所成之子空间。令 Φ Φ -->{\displaystyle \Phi } 为 V{\displaystyle V} 中长度为 2{\displaystyle {\sqrt {2}}} 的格子点。取 Rn+1{\displaystyle \mathbb {R} ^{n+1}} 的标准基 e1,… … -->,en+1{\displaystyle e_{1},\ldots ,e_{n+1}}，则根具有 ei− − -->ej(i≠ ≠ -->j){\displaystyle e_{i}-e_{j}\;(i\neq j)} 的形式，共有 n(n+1){\displaystyle n(n+1)} 个根。通常取单根为 α α -->i:=ei− − -->ei+1{\displaystyle \alpha _{i}:=e_{i}-e_{i+1}}。

对垂直于 α α -->i{\displaystyle \alpha _{i}} 的超平面的镜射在 Φ Φ -->{\displaystyle \Phi } 上的作用是交换第 i,i+1{\displaystyle i,i+1} 个座标。因此 An{\displaystyle A_{n}} 的外尔群不外就是对称群 Sn+1{\displaystyle S_{n+1}}。

An{\displaystyle A_{n}} 是李代数 sl(n+1,C){\displaystyle {\mathfrak {sl}}(n+1,\mathbb {C} )} 的根系。

Bn

取 V=Rn{\displaystyle V=\mathbb {R} ^{n}}，并令 Φ Φ -->{\displaystyle \Phi } 为 V{\displaystyle V} 中长度为 1,2{\displaystyle 1,{\sqrt {2}}} 的格子点。共有 2n2{\displaystyle 2n^{2}} 个根。通常取单根为 α α -->i=ei− − -->ei+1(1≤ ≤ -->in:=en{\displaystyle \alpha _{n}:=e_{n}}（短根）。

对短根 α α -->n{\displaystyle \alpha _{n}} 的反射即 (x1,… … -->,xn)↦ ↦ -->(x1,… … -->,− − -->xn){\displaystyle (x_{1},\ldots ,x_{n})\mapsto (x_{1},\ldots ,-x_{n})}。

B1{\displaystyle B_{1}} 跟 A1{\displaystyle A_{1}} 仅差一个缩放，因此通常仅考虑 n≥ ≥ -->2{\displaystyle n\geq 2} 的情形。Bn{\displaystyle B_{n}} 是李代数 so(2n+1,C){\displaystyle {\mathfrak {so}}(2n+1,\mathbb {C} )} 的根系。

Cn

取 V=Rn{\displaystyle V=\mathbb {R} ^{n}}，Φ Φ -->{\displaystyle \Phi } 为 V{\displaystyle V} 中所有长度 2{\displaystyle {\sqrt {2}}} 的格子点与形如 2λ λ -->{\displaystyle 2\lambda }的点，其中 λ λ -->{\displaystyle \lambda } 是长度为一的格子点。共有 2n2{\displaystyle 2n^{2}} 个根。通常取单根为 α α -->i:=ei− − -->ei+1(1≤ ≤ -->in:=2en{\displaystyle \alpha _{n}:=2e_{n}}（长根）。

C2{\displaystyle C_{2}} 与 B2{\displaystyle B_{2}} 仅差一个缩放加上旋转 45 度，因此通常仅考虑 n≥ ≥ -->3{\displaystyle n\geq 3} 的情形。Cn{\displaystyle C_{n}} 是李代数 sp(2n,C){\displaystyle {\mathfrak {sp}}(2n,\mathbb {C} )} 的根系。

Dn

取 V:=Rn{\displaystyle V:=\mathbb {R} ^{n}}，Φ Φ -->{\displaystyle \Phi } 为 V{\displaystyle V} 中长度 2{\displaystyle {\sqrt {2}}} 的格子点。共有 2n(n− − -->1){\displaystyle 2n(n-1)} 个根。通常取单根为 α α -->i=ei− − -->ei+1,(1≤ ≤ -->in=en+en− − -->1{\displaystyle \alpha _{n}=e_{n}+e_{n-1}}。

D3{\displaystyle D_{3}} 同构于 A3{\displaystyle A_{3}}，故通常仅考虑 n≥ ≥ -->4{\displaystyle n\geq 4} 的情形。Dn{\displaystyle D_{n}} 是李代数 so(2n,C){\displaystyle {\mathfrak {so}}(2n,\mathbb {C} )} 的根系。

E8, E7, E6

E8{\displaystyle E_{8}} 是较为特殊的根系。首先定义 R8{\displaystyle \mathbb {R} ^{8}} 中满足下述条件的点集 Γ Γ -->8{\displaystyle \Gamma _{8}}：

各座标均为整数，或均为半整数（不容相混）。

八个座标的和为偶数。

定义 E8{\displaystyle E_{8}} 为 Γ Γ -->8{\displaystyle \Gamma _{8}} 中长度为 2{\displaystyle {\sqrt {2}}} 的向量，即：

定义 E7{\displaystyle E_{7}} 为 E8{\displaystyle E_{8}} 与超平面 {x:(x,α α -->)=0}{\displaystyle \{x:(x,\alpha )=0\}} 之交， 其中 α α -->∈ ∈ -->E8{\displaystyle \alpha \in E_{8}} 是任取的根。同样步骤施于 E7{\displaystyle E_{7}}，得到更小的根系 E6{\displaystyle E_{6}}。根系 E6,E7,E8{\displaystyle E_{6},E_{7},E_{8}} 分别有 72, 126 与 240 个根。若续行此化约步骤，则会得到典型根系 D5,A4{\displaystyle D_{5},A_{4}}。

另一种等价的描述是取 Γ Γ -->8′{\displaystyle \Gamma "_{8}} 为：

各坐标均为整数，而且其和为偶数；或

各坐标均为半整数，而且其和为奇数。

Γ Γ -->8{\displaystyle \Gamma _{8}} 与 Γ Γ -->8′{\displaystyle \Gamma "_{8}} 同构。将任意偶数个座标乘以负一，便可在两者间转换。Γ Γ -->8{\displaystyle \Gamma _{8}} 称为 E8{\displaystyle E_{8}} 的偶坐标系，Γ Γ -->8′{\displaystyle \Gamma "_{8}} 称为奇坐标系。

在偶坐标下，通常取单根为

在奇坐标下，通常取单根为

（在上述定义中，若改取 β β -->3{\displaystyle \beta _{3}}，将得到同构的结果。若改取 β β -->1,β β -->7,β β -->2,β β -->6{\displaystyle \beta _{1},\beta _{7},\beta _{2},\beta _{6}}，将得到 A8{\displaystyle A_{8}} 或 D8{\displaystyle D_{8}}。至于 β β -->4{\displaystyle \beta _{4}}，其坐标和为零，而 α α -->1,… … -->,α α -->7{\displaystyle \alpha _{1},\ldots ,\alpha _{7}} 亦然，所以张出的向量空间维度不合所求。

删去 α α -->1{\displaystyle \alpha _{1}} 可得到 E7{\displaystyle E_{7}} 的一组单根；再删去 α α -->2{\displaystyle \alpha _{2}}，可得 E6{\displaystyle E_{6}} 的单根。

由于对 α α -->1{\displaystyle \alpha _{1}} 垂直等价于前两个坐标相等，而对 α α -->1,α α -->2{\displaystyle \alpha _{1},\alpha _{2}} 垂直等价于前三个座标相等，不难导出 E7,E6{\displaystyle E_{7},E_{6}} 的明确定义：

E7 = (α ∈ Z ∪ (Z+½): ∑αi + α1 = 2，∑αi + α1 ∈ 2Z),

E6 = (α ∈ Z ∪ (Z+½): ∑αi + 2α1 = 2，∑αi + 2α1 ∈ 2Z)

F4

对于 F4{\displaystyle F_{4}}，取 V=R4{\displaystyle V=\mathbb {R} ^{4}}，并令 Φ Φ -->{\displaystyle \Phi } 为满足下述条件的向量：

|α α -->|=1,2{\displaystyle |\alpha |=1,{\sqrt {2}}}

2α α -->{\displaystyle 2\alpha } 各坐标皆为奇数或皆为偶数。

此根系有 48{\displaystyle 48} 个根。通常取单根为 B3{\displaystyle B_{3}} 的单根再加上 α α -->4=− − -->(∑ ∑ -->i=14ei)/2{\displaystyle \alpha _{4}=-(\sum _{i=1}^{4}e_{i})/2}。

G2

G2{\displaystyle G_{2}} 有 12 个根，构成一个六边形的顶点，详如秩二的例子一节所示。通常取单根为

α α -->1{\displaystyle \alpha _{1}}

β β -->:=α α -->2− − -->α α -->1{\displaystyle \beta :=\alpha _{2}-\alpha _{1}}

在此沿用了之前的符号： α α -->i:=ei− − -->ei+1,(i=1,2){\displaystyle \alpha _{i}:=e_{i}-e_{i+1},\;(i=1,2)}。

根系与李群、李代数

不可约根系的分类可用于研究下述对象：

单复李代数

单复李群

模掉中心后为单李群的单连通复李群

紧单李群

文献

Serre, J.-P., Jones, G. A., Complex Semisimple Lie Algebras (2001), Springer-Verlag, ISBN 3540678271 .

Serre, J.-P. Lie Algebras and Lie Groups (2005), Lecture Notes in Mathematics, no. 1500, Springer-Verlag, ISBN 3540550089 .

Dynkin, E. B. The structure of semi-simple algebras. (Russian) Uspehi Matem. Nauk (N.S.) 2, (1947). no. 4(20), 59--127.

参见

外尔群，考克斯特群

考克斯特矩阵

ADE分类

根资料

考克斯特-邓肯图

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。