性质

Cn的另一个表达形式为Cn=(2nn)− − -->(2nn+1) for n≥ ≥ -->1{\displaystyle C_{n}={2n \choose n}-{2n \choose n+1}\quad {\mbox{ for }}n\geq 1} 所以，Cn是一个自然数；这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。（见下文的第二个证明。）

递推关系

它也满足

这提供了一个更快速的方法来计算卡塔兰数。

卡塔兰数的渐近增长为

它的含义是当n → ∞时，左式除以右式的商趋向于1。（这可以用n!的斯特灵公式来证明。）

所有的奇卡塔兰数Cn都满足n=2k− − -->1{\displaystyle n=2^{k}-1}。所有其他的卡塔兰数都是偶数。

应用

组合数学中有非常多的组合结构可以用卡塔兰数来计数。在Richard P. Stanley的Enumerative Combinatorics: Volume 2一书的习题中包括了66个相异的可由卡塔兰数表达的组合结构。以下用n=3和n=4举若干例：

Cn表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串，且所有的前缀字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:

将上例的X换成左括号，Y换成右括号，Cn表示所有包含n组括号的合法运算式的个数：

Cn表示有n个节点组成不同构二叉树的方案数。下图中，n等于3，圆形表示节点，月牙形表示什么都没有。

Cn表示有2n+1个节点组成不同构满二叉树（full binary tree）的方案数。下图中，n等于3，圆形表示内部节点，月牙形表示外部节点。本质同上。

证明：

令1表示进栈，0表示出栈，则可转化为求一个2n位、含n个1、n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有(2nn){\displaystyle {2n \choose n}}个，下面考虑不满足要求的数目。

考虑一个含n个1、n个0的2n位二进制数，扫描到第2m+1位上时有m+1个0和m个1（容易证明一定存在这样的情况），则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0，则对应一个n+1个0和n-1个1的二进制数。反之亦然（相似的思路证明两者一一对应）。

从而Cn=(2nn)− − -->(2nn+1)=1n+1(2nn){\displaystyle C_{n}={2n \choose n}-{2n \choose n+1}={\frac {1}{n+1}}{2n \choose n}}。证毕。

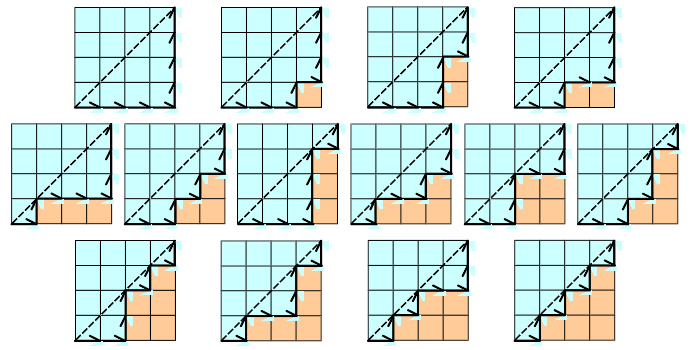
Cn表示所有在n × n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数：X代表“向右”，Y代表“向上”。下图为n = 4的情况：

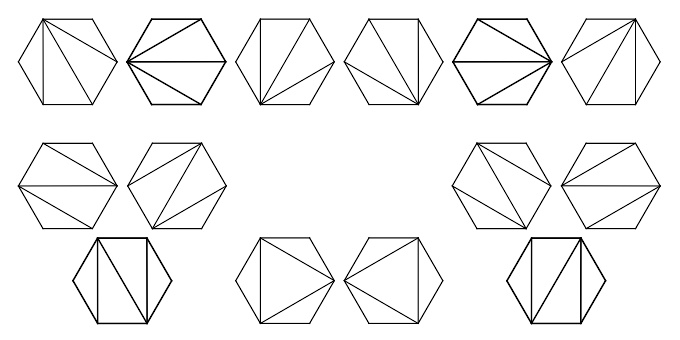
Cn表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数。下图中为n = 4的情况：

Cn表示对{1, ..., n}依序进出栈的置换个数。一个置换w是依序进出栈的当S(w) = (1, ..., n),其中S（w）递归定义如下：令w = unv，其中n为w的最大元素，u和v为更短的数列；再令S(w) = S(u)S(v)n，其中S为所有含一个元素的数列的单位元。

Cn表示集合{1, ..., n}的不交叉划分的个数.那么, Cn永远不大于第n项贝尔数. Cn也表示集合{1, ..., 2n}的不交叉划分的个数，其中每个段落的长度为2。综合这两个结论，可以用数学归纳法证明：在 魏格纳半圆分布定律 中度数大于2的情形下，所有 自由的累积量s 为零。 该定律在 自由概率论 和随机矩阵理论中非常重要。

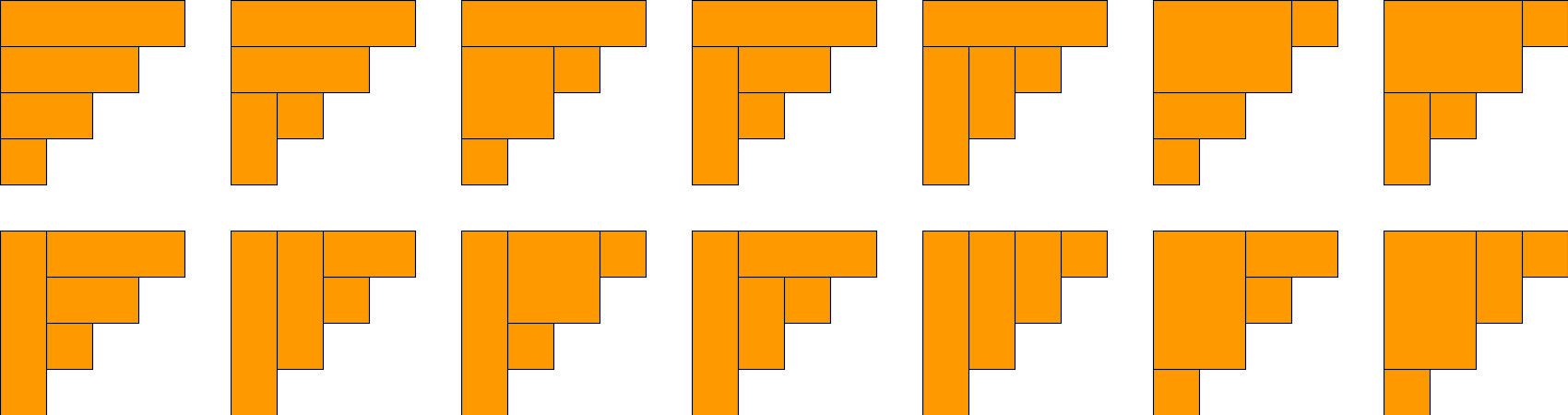
Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为n = 4的情况：

Cn表示表为2×n的矩阵的标准杨氏矩阵的数量。 也就是说，它是数字 1, 2, ..., 2n 被放置在一个2×n的矩形中并保证每行每列的数字升序排列的方案数。同样的，该式可由勾长公式的一个特殊情形推导得出。

Cn表示n个无标号物品的半序的个数。

汉克尔矩阵

无论n的取值为多少，n×n的汉克尔矩阵:Ai,j=Ci+j− − -->2. {\displaystyle A_{i,j}=C_{i+j-2}.\ }的行列式为1。例如，n = 4 时我们有

进一步，无论n的取值为多少，如果矩阵被移动成Ai,j=Ci+j− − -->1. {\displaystyle A_{i,j}=C_{i+j-1}.\ }，它的行列式仍然为1。 例如，n = 4 时我们有

同时，这两种情形合在一起唯一定义了卡塔兰数。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。