概念

电势移D{\displaystyle \mathbf {D} }的定义式为

其中，E{\displaystyle \mathbf {E} }是电场，P{\displaystyle \mathbf {P} }是电极化强度。

对于均向性的、线性的、均匀介电质，电极化强度P{\displaystyle \mathbf {P} }与电场E{\displaystyle \mathbf {E} }成正比：

其中，χ χ -->e{\displaystyle \chi _{e电极化率极化率

所以，电势移与电场的关系方程为

其中，ε ε -->{\displaystyle \varepsilon }是电容率。

假若，介电质是异向性的，则电容率是一个二阶张量，可用矩阵来表示。

一般而言，电容率不是常数，可以随着在介电质内的位置而改变，随着电场的频率、湿度、温度或其它参数而改变。对于一个非线性介电质，电容率有可能会随着电场强度而改变。当电容率是频率的函数时，它的数值有可能是实数，也有可能是复数。

真空电容率

“真空电容率”ε ε -->0{\displaystyle \varepsilon _{0}}是电势移与电场在真空里的比率，以方程定义为

其中，c{\displaystyle c}是光波在真空中的光速，μ μ -->0{\displaystyle \mu _{0}}是真空磁导率，μ μ -->0=4π π -->× × -->10− − -->7{\displaystyle \mu _{0}=4\pi \times 10^{-7}}。

在国际单位制里，常数c{\displaystyle c}和μ μ -->0{\displaystyle \mu _{0}}都是准确值（参阅NIST）。所以，关于米或安培这些物理量单位的数值设定，不能采用定义方式，而必须设计精密的实验来测量计算求得。由于π π -->{\displaystyle \无理数}是个无理数，ε ε -->0{\displaystyle \varepsilon _{0}}的数值只能够以近似值来表示。

真空电容率ε ε -->0{\displaystyle \varepsilon _{0}}也出现于库仑定律，是库仑常数1/4π π -->ε ε -->0{\displaystyle 1/4\pi \varepsilon _{0}}的一部分。所以，库仑常数也是一个准确值。

对于线性介质，电容率与真空电容率的比率，称为相对电容率ε ε -->r{\displaystyle \varepsilon _{r}}：

请注意，这公式只有在静止的、零频率的状况才成立。

对于各向异性材料，相对电容率是个张量；对于各向同性材料，相对电容率是个标量。

介质的电容率

对于常见的案例，均向性介质，D{\displaystyle \mathbf {D} }和E{\displaystyle \mathbf {E} }是平行的矢量，电容率ε ε -->{\displaystyle \varepsilon }是双折射双折射的二阶张量。介质的电容率和磁导率μ μ -->{\displaystyle \mu }，共同地决定了，电磁波相速度质时的相速度vp{\displaystyle v_{p}}：

对于线性介电质，电极化强度P{\displaystyle \mathbf {P} }与电场E{\displaystyle \mathbf {E} }成正比：

将这方程代入电势移的定义式，可以得到电势移与电场的关系式：

所以，电容率与电极化率的关系式为

复值电容率

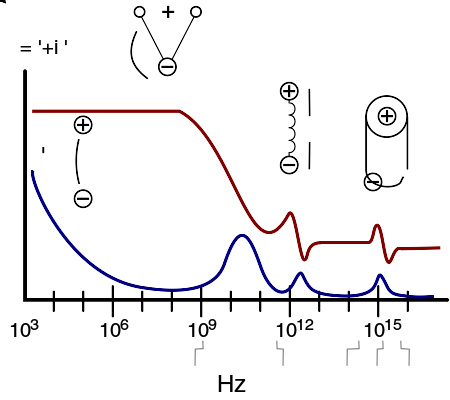
涵盖宽广频域的介电质的电容率频谱。ϵ ϵ -->′{\displaystyle \epsilon "}和ϵ ϵ -->″{\displaystyle \epsilon ""}分别标记电容率的实值部分和虚值部分。图内标示了几种电极化机制：离子导电、取向极化、原子极化、电子极化。

一般物质对于含时外电场的响应，跟真空的响应大不相同。一般物质的响应，通常跟外电场的频率有关。这属性反映出一个事实，那就是，由于物质具有质量，物质的电极化响应无法瞬时的跟上外电场。响应总是必需合乎因果关系，这需求可以以相位差来表达。因此，电容率时常以复函数来表达（复数允许同步的设定大小值和相位），而这复函数的参数为外电场频率ω ω -->{\displaystyle \omega }：ε ε -->→ → -->ε ε -->^ ^ -->(ω ω -->){\displaystyle \varepsilon \rightarrow {\widehat {\varepsilon }}(\omega )}。这样，电容率的关系式为

其中，D0{\displaystyle D_{0}}和E0{\displaystyle E_{0}}分别是电势移和电场的振幅。

请注意，时间相关性项目的正负号选择（指数函数的指数的正负号），决定了电容率虚值部分的正负号常规。在这里采用的正负号惯用于物理学；在工程学里，必须逆反所有虚值部分的正负号。

一个介电质对于静电场的响应，是由电容率的低频率极限来描述，又称为“静电容率”ε ε -->s{\displaystyle \varepsilon _{s}}：

在高频率极限，复电容率一般标记为 ε ε -->∞ ∞ -->{\displaystyle \varepsilon _{\infty }}。当频率等于或超过等离子体频率（plasma frequency）时，介电质的物理行为近似理想金属，可以用自由电子模型来计算交流电低频率交流电场，静电容率是个很好的近似。随着频率的增高，可测量到的相位差 δ δ -->{\displaystyle \delta }开始出现于D{\displaystyle \mathbf {D} }和E{\displaystyle \mathbf {E} }之间。出现时候的频率跟温度、介质种类有关。在中等的电场强度E0{\displaystyle E_{0}}状况，D{\displaystyle \mathbf {D} }和E{\displaystyle \mathbf {E} }保持成正比：

由于介质对于交流电场的响应特征是复电容率，为了更详细的分析其物理性质，很自然地，必须分离其实数和虚值部分，通常写为：

其中，虚值部分ε ε -->″{\displaystyle \varepsilon ""}关系到能量的耗散，而实值部分ε ε -->′{\displaystyle \varepsilon "}则关系到能量的储存。

由于复电容率是一个发生于多重频率的色散现象的叠加，其描述必须能够兼顾到这些色散现象。因此，复电容率通常会是一个相当复杂的、参数为频率的函数，称为“介电函数”。电容率ε ε -->^ ^ -->{\displaystyle {\widehat {\varepsilon }}}的极点必须匹配虚值部分为正值的频率，因此满足克拉莫-克若尼关系式。但是，在一般作业的狭窄频率值域内，电容率可以近似为跟频率无关，或者以适当的模型函数为近似。

物质分类

依据电容率和电导率σ σ -->{\displaystyle \sigma }，物质可以大致分为三类：导体、介电质、其它一般介质。高损耗物质会抑制电磁波的传播。通常，这些物质的 σ σ -->ω ω -->ε ε -->≫ ≫ -->1{\displaystyle {\frac {\sigma }{\omega \varepsilon }}\gg 1}，可以被视为优良导体。无损耗或低损耗物质，σ σ -->ω ω -->ε ε -->≪ ≪ -->1{\displaystyle {\frac {\sigma }{\omega \varepsilon }}\ll 1}，可以被视为介电质。其它不包括在这两种限制内的物质，被分类为一般介质。完美介电质是电导率等于0的物质，通常只允许有小量的位移电流存在。这种物质储存和归还电能的性质就好像理想电容器一样。

高损耗介质

对于高损耗介质案例，当传导电流不能被忽略时，总电流密度Jtot{\displaystyle J_{tot}}是

其中，Jc{\displaystyle J_{c}}是传导电流密度，Jd{\displaystyle J_{d}}是位移电流密度，σ σ -->{\displaystyle \sigma }是介质的电导率，ε ε -->{\displaystyle \varepsilon }是介质电容率的实值部分，ε ε -->^ ^ -->{\displaystyle {\widehat {\varepsilon }}}是介质的复电容率。

位移电流跟外电场E{\displaystyle E}的频率ω ω -->{\displaystyle \omega }有关。假若外电场是个静电场，则位移电流等于0。

采用这形式论，复电容率定义为

通常，介电质对于电磁能量有几种不同的吸收机制。受到这几种吸收机制的影响，随着频率的改变，电容率函数的样子也会有所改变(例:压电材料)。

弛豫（relaxation）效应发生于永久偶极分子和感应偶极分子。当频率较低的时候，电场的变化很慢。这允许偶极子足够的时间，对于任意时候的电场，都能够达成平衡状态。假若，因为介质的黏滞性，偶极子无法跟上频率较高的电场，电场能量就会被吸收，由而导致能量耗散。偶极子的这种弛豫机制称为介电质弛豫（dielectric relaxation）。理想偶极子的弛豫机制可以用经典的德拜弛豫（Debye relaxation）来描述。

共振效应是由原子、离子、电子等等的旋转或振动产生的。在它们特征吸收频率的附近，可以观察到这些程序。

上述两种效应时常会合并起来，使得电容器产生非线性效应。例如，当一个充电很久的电容器被短暂地放电时，它无法完全放电的效应称为“介电质吸收”。一个理想电容器，经过放电后，电压应该是0伏特。但是，实际的电容器会余留一些电压，称为“残余电压”。有些介电质，像各种不同的聚合物薄膜，残余电压小于原本电压的1-2%。但是，电解电容器（electrolytic capacitor）或超高电容器（supercapacitor）的残余电压可能会高达15 - 25%。

量子诠释

在量子力学里，电容率可以用发生于原子层次和分子层次的量子作用来解释。

在较低频率区域，极性介电质的分子会被外电场电极化，因而诱发出周期性转动。例如，在微波频率区域，微波场促使物质内的水分子做周期性转动。水分子与周边分子的相互碰撞产生了热能，使得含水分物质的温度增高。这就是为什么微波炉可以很有效率的将含有水分的物质加热。水的电容率的虚值部分（吸收指数）有两个最大值，一个位于微波频率区域，另一个位于远紫外线（UV）频率区域。这两个共振频率都高于微波炉的操作频率。

在中间频率区域，高过促使转动的频率区域，又远低于能够直接影响电子运动的频率区域，能量是以共振的分子振动形式被吸收。对于水介质，这是吸收指数开始显著地下降的区域。吸收指数的最低值是在蓝光频率区域（可见光谱段）。这就是为什么日光不会伤害像眼睛一类的含水生物组织。

在高频率区域（像远紫外线频率或更高频率），分子无法弛豫。这时，能量完全地被原子吸收，因而激发电子，使电子跃迁至更高能级，甚至游离出原子。拥有这频率的电磁波会导致电离辐射。

虽然，从开始到最后，对于物质的介电行为，做一个完全的计算机模拟，是一个可行之计。但是，这方法还没有得到广泛的使用。替代地，科学家接受现象模型为一个足以胜任的方法，可以用来捕捉实验行为。德拜弛豫和德拜–洛伦兹模型（Lorentz model）都是很优秀的模型。

测量

物质的电容率可以用几种静电测量方法来得到。使用各种各样的介电质光谱学（英语：Dielectric spectroscopy）（dielectric spectroscopy）方法，在广泛频率值域内，任何频率的复电容率都可以正确地评估出来。这频率值域覆盖接近21个数量级的大小值，从10 to 10赫兹。另外，使用低温恒温器（cryostat）和烤炉，科学家可以测量出，在不同的温度状况下，物质的介电性质。

椭圆偏振技术可以用在红外线频段和可见光频段。

也有一些方法用于介电常数的测量。介电常数在微波的范围可以由共振方法测量

参阅

高斯定律

磁化率

麦克斯韦方程组

克劳修斯-莫索提方程

进阶阅读

Theory of Electric Polarization: Dielectric Polarization, C.J.F. Böttcher, ISBN 0-444-41579-3

Dielectrics and Waves edited by A. von Hippel, Arthur R., ISBN 0-89006-803-8

Dielectric Materials and Applications edited by Arthur von Hippel, ISBN 0-89006-805-4

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。