简介

考虑一个具一般性的例子，有一个以下的方程：

其中x1,...,xn为未知数，而c为常数。其解为反像集合的成员

其中T1×···×Tn为函数ƒ的定义域。注意解集合可能为空集合（没有解）、单元素集合（唯一解）、有限个元素的集合及无限多个元素的集合（有无限多的解）。

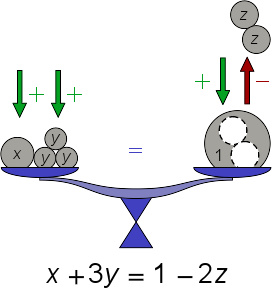
例如，以下的方程：

其未知数为x, y及z，可以在等式二侧同减21z，得到以下的式子：

以此例而言，方程不会只有唯一解，方程解的个数有无限多个，可以写为以下的集合

其中一个特殊解为x = 0, y = 0, z = 0，而x = 3, y = 6, z = 1和x = 8, y = 9, z = 2也是其解。解集合描述一个三维空间中，恰好穿过上述三个点的平面。

解集合

若解集合（英语：solution set）为空集合，表示不存在xi使得以下方程成立

其中c为一特定常数。

例如考虑一个经典的单变数例子，考虑定义域为整数的平方函数ƒ：

考虑以下方程

其解集合为{}，是空集合。因为2不是任何整数的平方，因此不可能找到整数可以使以上方程成立。但若修改函数的定义域，将其定义域改为所有实数，则上式有二个解，其解集合为

有些方程的解集合可能形成一个平面或曲面。例如在学习基础数学时，有提及形式为ax + by = c的方程，其中a, b, and c 都是实数的常数，且a和b至少有一个不为零，其解集合形成向量空间R中的一条直线。不过有些解集合不易用图解表示，例如ax + by + cz + dw = k（a, b, c, d, and k为实数的常数）的解集合会形成超平面。

相关条目

方程组

等化系数（英语：Equating coefficients）

数学分析

数值分析

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。