定义

点积有两种定义方式：代数方式和几何方式。通过在欧氏空间中引入笛卡尔坐标系，向量之间的点积既可以由向量坐标的代数运算得出，也可以通过引入两个向量的长度和角度等几何概念来求解。

代数定义

两个向量 a → → --> {\displaystyle {\vec {a}}} = [a1, a2, …, an]和 b → → --> {\displaystyle {\vec {b}}} = [b1, b2, …, bn]的点积定义为:

这里的Σ是求和符号，而n是向量空间的维数。

例如，两个三维向量[1, 3, -5]和[4, -2, -1]的点积是

点积还可以写为:

这里， b → → --> T {\displaystyle {\vec {b}}^{T}} 是矩阵 b → → --> {\displaystyle {\vec {b}}} 的转置，而 | a → → --> b → → --> T | {\displaystyle |{\vec {a}}{\vec {b}}^{T}|} 是 a → → --> b → → --> T {\displaystyle {\vec {a}}{\vec {b}}^{T}} 的行列式。

使用上面的例子，一个1×3矩阵（行向量）乘以一个3×1矩阵（列向量）的行列式就是结果(通过矩阵乘法得到1×1矩阵，再利用行列式得出标量答案):

几何定义

在欧几里得空间中，点积可以直观地定义为

这里 | x → → --> {\displaystyle {\vec {x}}} | 表示 x → → --> {\displaystyle {\vec {x}}} 的模（长度），θ表示两个向量之间的角度。

注意：点积的形式定义和这个定义不同；在形式定义中， a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b}}} 的夹角是通过上述等式定义的。

这样，两个互相垂直的向量的点积总是零。若 a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b单位向量都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。那么，给定两个向量，它们之间的夹角可以通过下列公式得到：

这个运算可以简单地理解为：在点积运算中，第一个向量投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。

标量投影

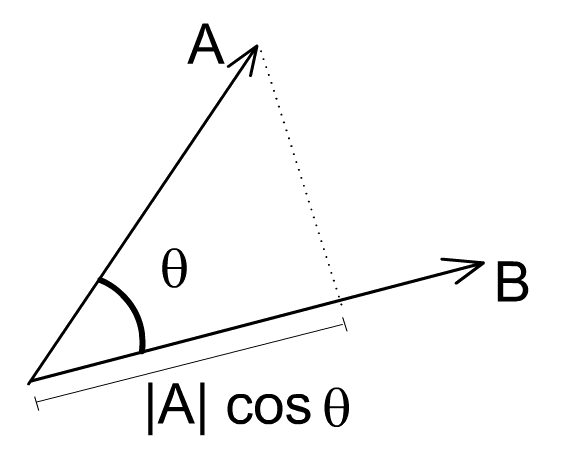
 A·B = |A| |B| cos(θ). |A| cos(θ)是A到B的投影。

欧氏空间中向量A在向量B上的标量投影是指

这里 θ 是A 和 B的夹角。 从点积的几何定义 A ⋅ ⋅ --> B = | A | | B | cos ⁡ ⁡ --> θ θ --> {\displaystyle \mathbf {A} \cdot \mathbf {B} =|\mathbf {A} ||\mathbf {B} |\cos \theta } 不难得出，两个向量的点积: A ⋅ ⋅ --> B {\displaystyle \mathbf {A} \cdot \mathbf {B} } 可以理解为向量 A {\displaystyle \mathbf {A} } 在向量 B {\displaystyle \mathbf {B} } 上的投影再乘以B的长度。

两种定义的等价性

点积的两种定义中，只需给定一种定义，另外一种定义就可以推出。

由几何定义推出代数定义

设e1, …, en 是 R 空间的一组标准正交基, 可以得出：

上文中已经得知两个向量点积的几何定义实际上就是一个向量在另外一个向量上的投影，故A在任一标准基en 的点积 A ⋅ ⋅ --> e i {\displaystyle \mathbf {A} \cdot \mathbf {e} _{i}} 就是A在此标准基向量上的投影，而根据向量自身的定义，这个投影即为ai 。因此：

由代数定义推出几何定义

应用余弦定理。 注意：这个证明采用三维向量，但可以推广到n维的情形。

考虑向量

重复使用勾股定理得到

而由代数定义

所以，根据向量点积的代数定义，向量 v → → --> {\displaystyle {\vec {v}}} 和自身的点积就是其长度的平方。

现在，考虑两个从原点出发的向量 a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {b}}} ，夹角θ。第三个向量 c → → --> {\displaystyle {\vec {c}}} 定义为

构造以 a → → --> {\displaystyle {\vec {a}}} ， b → → --> {\displaystyle {\vec {b}}} ， c → → --> {\displaystyle {\vec {c}}} 为边的三角形，采用余弦定理，有

根据引理1，用点积代替向量长度的平方，有

同时，根据定义 c → → --> {\displaystyle {\vec {c}}} ≡ a → → --> {\displaystyle {\vec {a}}} - b → → --> {\displaystyle {\vec {b}}} ，有

根据分配律，得

连接等式 （1）和 （2）有

简化等式即得

以上即为向量点积的几何定义。

需要注意的是，点积的几何解释通常只适用于 R n {\displaystyle \mathbb {R} ^{n}} ( n ≤ ≤ --> 3 {\displaystyle n\leq 3} )。在高维空间，其他的域或模中，点积只有一个定义，那就是

点积可以用来计算合力和功。若 b → → --> {\displaystyle {\vec {b}}} 为单向量，则点积即为 a → → --> {\displaystyle {\vec {a}}} 在方向 b → → --> {\displaystyle {\vec {b}}} 的投影，即给出了力在这个方向上的分解。功即是力和位移的点积。

性质

点积满换律： a → → --> ⋅ ⋅ --> b → → --> = b → → --> ⋅ ⋅ --> a → → --> {\displaystyle {\vec {a}}\cdot {\vec {b}}={\vec {b}}\cdot {\vec {a}}\;}

点积满足分配律: a → → --> ⋅ ⋅ --> ( b → → --> + c → → --> ) = a → → --> ⋅ ⋅ --> b → → --> + a → → --> ⋅ ⋅ --> c → → --> {\displaystyle {\vec {a}}\cdot ({\vec {b}}+{\vec {c}})={\vec {a}}\cdot {\vec {b}}+{\vec {a}}\cdot {\vec {c}}}

点积是个双线性算子： a → → --> ⋅ ⋅ --> ( r b → → --> + c → → --> ) = r ( a → → --> ⋅ ⋅ --> b → → --> ) + ( a → → --> ⋅ ⋅ --> c → → --> ) {\displaystyle {\vec {a}}\cdot (r{\vec {b}}+{\vec {c}})=r({\vec {a}}\cdot {\vec {b}})+({\vec {a}}\cdot {\vec {c}})\;}

在乘以一个标量的时候点积满足: ( c 1 a → → --> ) ⋅ ⋅ --> ( c 2 b → → --> ) = ( c 1 c 2 ) ( a → → --> ⋅ ⋅ --> b → → --> ) {\displaystyle (c_{1}{\vec {a}})\cdot (c_{2}{\vec {b}})=(c_{1}c_{2})({\vec {a}}\cdot {\vec {b}})}

(后两个性质从前两个得出)。

两个非零向量 a → → --> {\displaystyle {\vec {a}}} 和 b → → --> {\displaystyle {\vec {垂直}} 是垂直的，当且仅当 a → → --> {\displaystyle {\vec {a}}} · b → → --> {\displaystyle {\vec {b}}} = 0。

如果 b → → --> {\displaystyle {\vec {b}}} 是单位向量，则点积给出 a → → --> {\displaystyle {\vec {a}}} 在方向 b → → --> {\displaystyle {\vec {b}}} 上投影的大小，如果方向相反则带有负号。分解向量对求向量的和经常是有用的，比如在力学中计算合力。

不像普通数的乘法服从消去律，如果ab = ac，则b总是等于c，除非a等于零。而对于点积:

应用

物理学中力学的力做功的问题，经常用到点积计算。

计算机图形学常用来进行方向性判断，如两向量点积大于0，则它们的方向朝向相近；如果小于0，则方向相反。

向量内积是人工智能领域中的神经网络技术的数学基础之一。

此方法被用于动画渲染（Animation-Rendering）。

广义定义

在一个向量空间 V {\displaystyle V} 中，定义在 V × × --> V {\displaystyle V\times V} 上对称定对称双线性形式函数即是 V {\displaystyle V} 的数量积，而添加有一个数量积的向量空间即是内积空间。

参见

向量积

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。