参见圆概率误差信度（英语：reliability）与效度（英语：validity）

含义“科学”不好以简短文字加以准确定义。一般说来，科学涵盖三方面含义：观察：致力于揭示自然真相，而对自然作用由充分的观察或研究（包括思想实验），通常指可通过必要的方法进行的，或能通过科学方法——一套用以评价经验知识的程序而进行的。假设：通过这样的过程假定组织体系知识的系统性。检证：借此验证研究目标的信度与效度。科学包括基础科学与应用科学。基础科学仅以通过试验探究自然原理为目的，其成果一般不容易在短期内得到应用，如物理、化学、生物和地质学；应用科学则兼有探究原理与关注应用这两个方面的动机，如医学、药学、应用光学、气象学、科技考古学和博弈论。按理来说，科学不同于纯技术类学科，后者只涉及运用已有的知识与原理进行发明创造，而只带来技术变革，不在原理层次挖掘出的新规律，如工程学、法医学、农学和林学。应用科学与纯技术有时候很难界定。因科学与技术经常一起被提及，重要的技术发展有时也会被大众视为是科学成就...

历史1883年6月的一期封面1880年，纽约新闻记者约翰·迈克尔斯（英语：JohnMichaels）创立了《科学》，这份期刊先后得到了托马斯·爱迪生以及亚历山大·格拉汉姆·贝尔的资助。但由于从未拥有足够的用户而难以为继，《科学》于1882年3月停刊。一年后，昆虫学家SamuelHubbardScudder使其复活并取得了一定的成功。然而到了1894年，《科学》重新陷入财政危机，随后被以500美元的价格转让给心理学家JamesMcKeenCattell。1900年，Cattell与美国科学促进会秘书LelandOssianHoward达成协议，《科学》成为美国科学促进会的期刊。在20世纪早期，《科学》发表的重要文章包括托马斯·亨特·摩根的果蝇遗传、阿尔伯特·爱因斯坦的引力透镜以及埃德温·哈勃的螺旋星系。1944年Cattell去世后，AAAS成为《科学》新主人。争议在2002年，《科学》期刊...

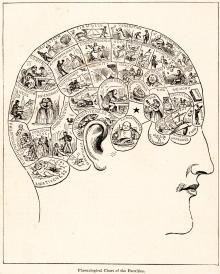
总览科学方法论典型的十九世纪颅相学挂图：在十九世纪20年代，颅相学家声称意志可以存在于大脑的各个部位。他们对人格特征的阅读在之后被证伪。1843年，颅相学第一个被定为伪科学。虽然用以证明某一知识体系、方法论、或实践时科学的标准千差万别，但基本理论是一致的。其基本观点是所有的科学结果必须是可重复的，并可由他人进行主体间可验证性。这些原则旨在保证实验可以在同等条件下重复，使得进一步对某一现象的假说或理论是有效的、可靠的。标准要求至始至终贯彻科学凡事，误差应得到控制，或通过随机性、适当例样、双盲研究或其它方式来消除。得到的所有数据，包括实验和环境状况，都应备案，以便同行评审，允许更进一步的实验研究来证明或证伪。统计量化的显著性差异、置信区间、误差范围都是重要的科学研究工具。可证伪性到了二十世纪中叶，卡尔·波普尔将可证伪性视为科学和伪科学的标准。可证伪性意味着结果可以被证伪。例如，论断“上帝创造了...

应用计算科学的问题域包括：数值模拟数值模拟有各种不同的目的，取决于被模拟的任务的特性：重建和理解已知事件（如地震、海啸和其他自然灾害）。预测未来或未被观测到的情况（如天气、亚原子粒子的行为）。模型拟合与数据分析适当调整模型或利用观察来解方程，不过也需要服从模型的约束条件（如石油勘探地球物理学、计算语言学）。利用图论创建网络的模型，特别是那些相互联系的个人、组织和网站的模型。计算优化最优化已知方案（如工艺和制造过程、前端工程学）。方法和算法计算科学中的算法和数学方法是多样的，常用的应用方法包括：数值分析作为收敛和渐近级数的泰勒级数的应用利用自动微分计算微分利用有限差计算微分图论集凭借泰勒级数和理查森外推法进行高阶微分逼近均匀网格上的积分方法：矩形法、梯形法、中点法和辛普森积分法龙格－库塔法解常微分方程蒙特卡洛方法分子动力学数值线性代数用高斯消元法计算LU因子乔里斯基分解离散傅里叶变换及应用牛...