基尔霍夫积分定理
导引
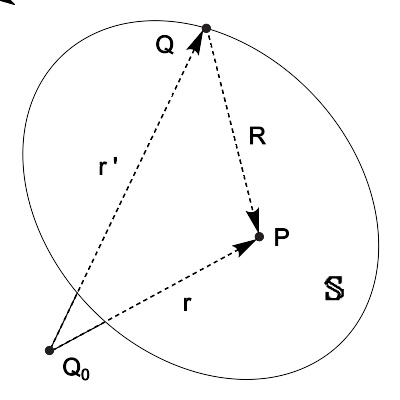
点P被包围在闭合曲面S{\displaystyle \mathbb {S} }内。
根据格林第二恒等式,假若在体积V{\displaystyle \mathbb {V} }内,函数ϕ ϕ -->{\displaystyle \phi }和ψ ψ -->{\displaystyle \psi }都是二次连续可微,则
其中,闭合曲面S{\displaystyle \mathbb {S} }是体积V{\displaystyle \mathbb {V} }的表面,dS{\displaystyle \mathrm {d} \mathbf {S} }是从闭合曲面S{\displaystyle \mathbb {S} }向外指出的微小面元素矢量。
这方程的左手边是积分于体积V{\displaystyle \mathbb {V} },右手边是积分于这体积的闭合曲面S{\displaystyle \mathbb {S} }。
设定函数ψ ψ -->(r){\displaystyle \psi (\mathbf {r} )}满足单色波的亥姆霍兹波动方程:
设定ϕ ϕ -->(r,r′){\displaystyle \phi (\mathbf {r} ,\mathbf {r} ")}为一种格林函数,是可以描述自由于自由空间、满足数值在无穷远为零的边界条件的圆球面出射波:
其中,R=|r− − -->r′|{\displaystyle R=|\mathbf {r} -\mathbf {r} "|}。
这函数ϕ ϕ -->(r,r′){\displaystyle \phi (\mathbf {r} ,\mathbf {r} ")}满足关系式
其中,δ δ -->(r− − -->r′){\displaystyle \delta (\mathbf {r} -\mathbf {r} ")}是三维狄拉克δ函数。
将ϕ ϕ -->(r,r′){\displaystyle \phi (\mathbf {r} ,\mathbf {r} ")}、ψ ψ -->(r){\displaystyle \psi (\mathbf {r} )}的满足式代入,则格林第二恒等式变为
为了标记原因,对换无单撇号与有单撇号的变量。这样,r{\displaystyle \mathbf {r} }标记检验位置,r′{\displaystyle \mathbf {r} "}标记源位置:
假若波扰r{\displaystyle \mathbf {r} }的位置在体积V{\displaystyle \mathbb {V} }内,即点P被包围在闭合曲面S{\displaystyle \mathbb {S} }内,则ψ ψ -->(r){\displaystyle \psi (\mathbf {r} )}写为
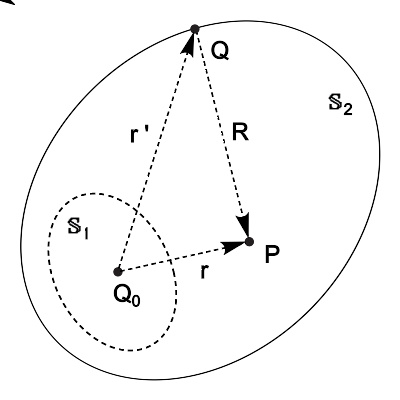
闭合曲面S{\displaystyle \mathbb {S} }是由闭合曲面S1{\displaystyle \mathbb {S} _{1}}与闭合曲面S2{\displaystyle \mathbb {S} _{2}}共同组成。点P处于曲面S1{\displaystyle \mathbb {S} _{1}}之内,曲面S2{\displaystyle \mathbb {S} _{2}}之外。
上述公式应用于点P被包围在闭合曲面内的物理案例,即从位于闭合曲面的次波源所发射出的次波,在闭合曲面内的点P所产生的波扰。大多数衍射案例计算,从延伸尺寸波源发射出的波,其波前所形成的闭合曲面,在闭合曲面的所有次波源,所发射出的次波,在闭合曲面外的点P所产生的波扰;对于这些案例,点P在闭合曲面之外,延伸波源在闭合曲面之内。这公式也可以推导为点P在闭合曲面外,波源在闭合曲面之内的物理案例。如右图所示,假设闭合曲面S{\displaystyle \mathbb {S} }是由闭合曲面S1{\displaystyle \mathbb {S} _{1}}与闭合曲面S2{\displaystyle \mathbb {S} _{2}}共同组成,曲面S1{\displaystyle \mathbb {S} _{1}}被包围在曲面S2{\displaystyle \mathbb {S} _{2}}的内部。点P处于曲面S2{\displaystyle \mathbb {S} _{2}}之内,曲面S1{\displaystyle \mathbb {S} _{1}}之外。
让曲面S2{\displaystyle \mathbb {S} _{2}}的半径趋于无穷大,则对于曲面S2{\displaystyle \mathbb {S} _{2}}的任意点Q,R→ → -->r′{\displaystyle R\to r"}、R^ ^ -->→ → -->− − -->r′^ ^ -->{\displaystyle {\hat {\mathbf {R} }}\to -{\hat {\mathbf {r} "}}},被积函数趋向于零,快过r′{\displaystyle r"}平方反比的趋向于零,满足“索莫菲辐射条件”(Sommerfeld radiation condition),因此在曲面S2{\displaystyle \mathbb {S} _{2}}的总贡献为零。所以,在点P的波扰为
注意到微小面元素矢量dS′{\displaystyle \mathrm {d} \mathbf {S} "}的方向是从曲面S1{\displaystyle \mathbb {S} _{1}}向内指入。现在,将微小面元素矢量dS′{\displaystyle \mathrm {d} \mathbf {S} "}的方向改为与原本方向相反:dS′→ → -->− − -->dS′{\displaystyle \mathrm {d} \mathbf {S} "\to -\mathrm {d} \mathbf {S} "},即从闭合曲面S1{\displaystyle \mathbb {S} _{1}}向外指基尔霍夫得到基尔霍夫积分定理的表达式:
假设η η -->^ ^ -->{\displaystyle {\hat {\boldsymbol {\eta }}}}是与dS′{\displaystyle \mathrm {d} \mathbf {S} "}同方向的单位矢量,是垂直于闭合曲面S1{\displaystyle \mathbb {S} _{1}}的法矢量。那么,法向导数与梯度的关系为
所以,基尔霍夫积分定理的另一种表达式为
总结,只考虑单色波,位于点P的波扰ψ ψ -->(r){\displaystyle \psi (\mathbf {r} )},可以以位于闭合曲面S1{\displaystyle \mathbb {S} _{1}}的所有波扰ψ ψ -->(r′){\displaystyle \psi (\mathbf {r}梯度)}与其梯度∇ ∇ -->′ψ ψ -->(r′){\displaystyle \nabla "\psi (\mathbf {r} ")}来表达。
非单色波
对于非单色波,必须使用更广义的形式。以傅里叶积分来表达非单色波的分解:
其中,ω ω -->=kc{\displaystyle \omega =kc}是角速度,c{\displaystyle c}是光速。
根据傅里叶反演公式(Fourier inversion formula):
对于每一个傅里叶分量ψ ψ -->ω ω -->{\displaystyle \psi _{\omega }},应用基尔霍夫积分定理,可以得到
将这公式代入Ψ Ψ -->(r,t){\displaystyle \Psi (\mathbf {r} ,t)}的傅里叶积分公式:
设定k=ω ω -->/c{\displaystyle k=\omega /c},注意到推迟时间tr=t− − -->R/c{\displaystyle t_{r}=t-R/c}出现在相位因子里,必须将光波传播的时间纳入计算。更换积分次序,公式变为
在时间t{\displaystyle t},位于点P的波扰Ψ Ψ -->(r,t){\displaystyle \Psi (\mathbf {r} ,t)},可以以位于闭合曲面S{\displaystyle \mathbb {S} }的所有波扰在其推迟时间tr{\displaystyle t_{r}}的数值Ψ Ψ -->(r′,tr){\displaystyle \Psi (\mathbf {r} ",t_{r})}与其法向导数∂ ∂ -->Ψ Ψ -->(r′,tr)/∂ ∂ -->n′{\displaystyle \partial \Psi (\mathbf {r} ",t_{r})/\partial n"}来表达:
这就是推广后的基尔霍夫积分定理。
标量理论
光波是传播于空间的电磁辐射,理当被视为一种电磁场矢量现象。但是,基尔霍夫的理论是标量理论,将光波当作标量处理,这可能会造成偏差。因此,物理学者做了很多实验来检查结果是否准确。他们发现,只要孔径尺寸比波长大很多、孔径与观察屏之间的距离不很近,则使用标量理论可以得到相当准确的答案。但是对于某些问题,例如高分辨率光栅衍射,标量理论就不适用,必须使用矢量理论。
参阅
衍射
泊松光斑
推迟势
李纳-维谢势
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值



24小时热门
推荐阅读



关于我们

APP下载







































