惠更斯原理

惠更斯原理是克里斯蒂安·惠更斯于1678年提出的关于波传播的理论。惠更斯原理表明，假设在时间 t = t 0 {\displaystyle t=t_{0}} 由主波源Q 0 发射出的球面波，在时间 t = t 1 {\displaystyle t=t_{1}} 传播到波前 S {\displaystyle \mathbb {S} } ，那么位于波前 S {\displaystyle \mathbb {S} } 的每一个面元素矢量 d S {\displaystyle \mathrm {d} \mathbf {S} } 都可以被视为一个次波源，所有从这些次波源发射出的次波，在之后时间 t = t 2 {\displaystyle t=t_{2}} 波前的包络面就是主波源Q 0 所发射出的球面波在时间 t = t 2 {\displaystyle t=t_{2}} 的波前。

惠更斯-菲涅耳原理

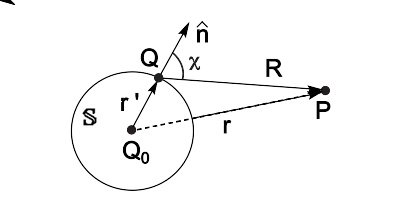
从主波源Q 0 发射出的球面波，其波前 S {\displaystyle \mathbb {S} } 的每一点Q都可以视为次波源，它们会发射出次波，在空间任意一点P的波扰是所有这些次波在该点P的相干叠加。

波动有两个基本属性：

惠更斯原理只阐述了前一条属性，奥古斯丁·菲涅耳将惠更斯提出的次波的概念加以延伸，提出用“次波相干叠加”的点子来解释衍射现象，这就是惠更斯-菲涅耳原理。这原理表明，波前 S {\displaystyle \mathbb {S} } 的每个面元素矢量 d S ′ {\displaystyle \mathrm {d} \mathbf {S} "} 都可以视为次波源，它们会发射出次波，在空间任意一点P的波扰是所有这些次波在该点P的相干叠加。设定位于波前 S {\displaystyle \mathbb {S} } 的任意一点Q，它在点P贡献的复振幅为 d ψ ψ --> ( r , r ′ ) {\displaystyle \mathrm {d} \psi (\mathbf {r} ,\mathbf {r} ")} ；其中， r {\displaystyle \mathbf {r} } 、 r ′ {\displaystyle \mathbf {r} "} 分别为点P、点Q的位置。在点P的总波扰为

为了将这公式具体化，菲涅耳凭借直觉对 d ψ ψ --> ( r , r ′ ) {\displaystyle \mathrm {d} \psi (\mathbf {r} ,\mathbf {r} ")} 作出了如下假设：

它应当正比于面元素的面积：

它应当正比于次波源的复振幅：

次波源发射出的次波应是球面波，其中 k {\displaystyle k} 是波数：

次波源发射出的次波是各向异性的。假设 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 是与面元素矢量 d S ′ {\displaystyle \mathrm {d} \mathbf {S} "} 同方向的单位矢量， χ χ --> {\displaystyle \chi } 是 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 与 R ^ ^ --> {\displaystyle {\hat {\mathbf {R} }}} 之间的夹角，则倾斜因子 K ( χ χ --> ) {\displaystyle K(\chi )} 与 d ψ ψ --> ( r , r ′ ) {\displaystyle \mathrm {d} \psi (\mathbf {r} ,\mathbf {r} ")} 的关系为

根据以上假设可以得到如下菲涅耳衍射积分公式

其中， c {\displaystyle c} 是比例常数。

菲涅耳-基尔霍夫衍射公式

在菲涅耳衍射积分公式提出六十余年后，古斯塔夫·基尔霍夫用严格的数学理论推导出菲涅耳-基尔霍夫衍射公式：

其中， α α --> {\displaystyle \alpha } 、 χ χ --> {\displaystyle \chi } 分别是 r ′ ^ ^ --> {\displaystyle {\hat {\mathbf {r} "}}} 、 R ^ ^ --> {\displaystyle {\hat {\mathbf {R} }}} 与 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 之间的夹角。

推论从点光源Q 0 发射的单色光波，其波扰的数值大小与传播距离成反比，在位置 r ′ {\displaystyle \mathbf {r} "} 以方程表达为 ψ ψ --> ( r ′ ) = ψ ψ --> 0 e i k r ′ / r ′ {\displaystyle \psi (\mathbf {r} ")=\psi _{0}e^{ikr"}/r"} 。又在其发射出的球面波的波前任意位置， r ′ ^ ^ --> {\displaystyle {\hat {\mathbf {r} "}}} 与 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 同向，夹角 α α --> = 0 {\displaystyle \alpha =0} 。设定比例常数 c = − − --> i / λ λ --> {\displaystyle c=-i/\lambda } ， K ( χ χ --> ) = ( 1 + cos ⁡ ⁡ --> χ χ --> ) / 2 {\displaystyle K(\chi )=(1+\cos \chi )/2} ，则可得到菲涅耳衍射积分公式。

严格导引

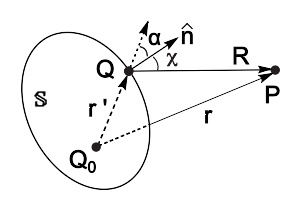
点P在闭合曲面 S {\displaystyle \mathbb {S} } 之外。位于点P的波扰 ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} ，可以以位于闭合曲面 S {\displaystyle \mathbb {S} } 的所有波扰与其梯度表达。

基尔霍夫积分定理应用格林第二恒等式来推导出齐次波动方程的解答，这解答是以波动方程在任意闭合曲面 S {\displaystyle \mathbb {S} } 的每一个点的解答和其一阶导数来表达。

对于单频率波，解答为

或者

其中， r {\displaystyle \mathbf {r} } 、 r ′ {\displaystyle \mathbf {r} "} 分别是从点Q 0 到点P、点Q的位移矢量， ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} 是在点P的波扰， R = r − − --> r ′ {\displaystyle \mathbf {R} =\mathbf {r} -\mathbf {r} "} 是从点Q到点P的位移矢量， R {\displaystyle R} 是其数值大小， k {\displaystyle k} 是波数， ∇ ∇ --> ′ {\displaystyle \nabla "} 是对于源位置 r ′ {\displaystyle \mathbf 梯度} "} 的梯度， d S ′ {\displaystyle \mathrm {d} \mathbf {S} "} 是从闭合曲面 S {\displaystyle \mathbb {S} } 向外指出的微小面元素矢量， ∂ ∂ --> ∂ ∂ --> n ′ {\displaystyle {\frac {\partial }{\partial n"}}} 是闭合曲面 S {\displaystyle \mathbb {S} } 的法向导数。

在推导基尔霍夫衍射公式的过程中，基尔霍夫做了以下假定：

点波源与孔隙之间的距离 r ′ {\displaystyle r"} 超大于波长 λ λ --> = 2 π π --> / k {\displaystyle \lambda =2\pi /k} 。

R {\displaystyle R} 超大于波长 λ λ --> {\displaystyle \lambda } 。

点波源

从点波源Q 0 发射的单频率波，其能量与传播距离平方成反比，波扰的数值大小与传播距离成反比，在点Q的波扰以方程表达为

其中， ψ ψ --> 0 {\displaystyle \psi _{0}} 是复值波幅。

假设点P在闭合曲面 S {\displaystyle \mathbb {S} } 之外，应用基尔霍夫积分定理的方程，可以得到在点P的波扰：

其中， n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 是与 d S ′ {\displaystyle \mathrm {d} \mathbf {S} "} 同方向的单位矢量。

注意到球面出射波的梯度为

从基尔霍夫所做的假定， k ≫ ≫ --> 1 / R {\displaystyle k\gg 1/R} 、 k ≫ ≫ --> 1 / r ′ {\displaystyle k\gg 1/r"} （例如，假设距离大约为1mm，则对于波长在0.4μm至0.可见光之间的可见光，可以做这假定；但对于波长在1mm微波m之间的微波，这假定不适用），则上述两个公式近似为

所以，在点P的波扰

其中， α α --> {\displaystyle \alpha } 、 χ χ --> {\displaystyle \chi } 分别是 r ′ ^ ^ --> {\displaystyle {\hat {\mathbf {r} "}}} 、 R ^ ^ --> {\displaystyle {\hat {\mathbf {R} }}} 与 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 之间的夹角。

这就是菲涅耳-基尔霍夫衍射公式，或 基尔霍夫衍射公式 。

倾斜因子

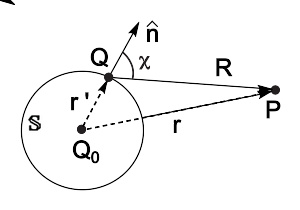
倾斜因子 K ( χ χ --> ) {\displaystyle K(\chi )} 为 [ 1 + cos ⁡ ⁡ --> ( χ χ --> ) ] / 2 {\displaystyle [1+\cos(\chi )]/2} 。

如右图所示，假设闭合曲面 S {\displaystyle \mathbb {S} } 是圆球面，点波源Q 0 与圆球面 S {\displaystyle \mathbb {S} } 的圆心同点。在圆球面 S {\displaystyle \mathbb {S} } 的任意位置， r ′ ^ ^ --> {\displaystyle {\hat {\mathbf {r} "}}} 与 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 同向，所以，

注意到 r ′ {\displaystyle r"} 是圆球面 S {\displaystyle \mathbb {S} } 的半径，对于这积分， r ′ {\displaystyle r"} 值不变，可以从积分里提出。在点P的波扰为

其中， K ( χ χ --> ) = 1 + cos ⁡ ⁡ --> χ χ --> 2 {\displaystyle K(\chi )={\frac {1+\cos \chi }{2}}} 为倾斜因子。

应用惠更斯－菲涅耳原理，所得到在点P的波扰的方程，就是这方程。但是，惠更斯－菲涅耳原理无法解释相位差与倾斜因子的物理原因。倾斜因子使得次波的波幅会因为传播方向而不同；朝着主波方向，波幅较大；逆着主波方向，波幅较小。这解释了为什么波动只会朝着前方传播的物理现象。

惠更斯－菲涅耳原理

仔细诠释惠更斯－菲涅耳原理的方程：从点波源Q 0 发射的波幅为 ψ ψ --> 0 {\displaystyle \psi _{0}} 的球面波，在点Q的波扰为 ψ ψ --> ( r ′ ) = ψ ψ --> 0 e i k r ′ / r ′ {\displaystyle \psi (\mathbf {r} ")=\psi _{0}e^{ikr"}/r"} ；而从点Q发射的次波，将倾斜因子与相位差纳入考量，所贡献出的波扰，在点P为

总合所有与点Q同波前的点次波源在点P所贡献出的波扰，就可以得到 ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} 。

换另一种直接方法来诠释，从点波源Q 0 发射的球面波，在点P的波扰为

假若这两种诠释都正确，则从这两种 ψ ψ --> ( r ) {\displaystyle \psi (\mathbf {r} )} 的表达式分别计算出的结果，应该可以被核对为相等：

为了简易计算，假设 r ≫ ≫ --> r ′ {\displaystyle r\gg r"} ，则以下近似成立：

其中， θ θ --> {\displaystyle \theta } 为 r ′ {\displaystyle \mathbf {r} "} 与 r {\displaystyle \mathbf {r} } 之间的夹角。

所以，在点P的波扰可以近似为

有限尺寸波源

假设波源为有限尺寸，位于曲面 S {\displaystyle \mathbb {S} } 的波扰表达为 ψ ψ --> ( r ′ ) {\displaystyle \psi (\mathbf {r} ")} ，则位于点P的波扰为

假定 k ≫ ≫ --> 1 / R {\displaystyle k\gg 1/R} ，则

这是基尔霍夫衍射公式最广义的形式。解析涉及到有限尺寸波源的问题，必须用体积分来将波源的每一点所给出的贡献总合在一起。

标量理论

光波是传播于空间的电磁辐射，理当被视为一种电磁场矢量现象。但是，基尔霍夫的理论是标量理论，将光波当作标量处理，这可能会造成偏差。因此，物理学者做了很多实验来检查结果是否准确。他们发现，只要孔径尺寸比波长大很多、孔径与观察屏之间的距离不很近，则使用标量理论可以得到相当准确的答案。但是对于某些问题，例如高分辨率光栅衍射，标量理论就不适用，必须使用矢量理论。

参阅

泊松光斑

基尔霍夫衍射公式

基尔霍夫积分定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。