近心点经度

由状态向量计算在太空动力学，昇交点经度可以从轨道状态向量计算如下：此处，n=（nx,ny,nz）是指向升交点的向量。参考平面是假设的xy-平面，经度原点的位置在+x-轴的方向。对无倾斜轨道（轨道倾斜角为0度）就无须定义Ω。计算时依惯例设为0，也就是说指向昇交点的向量n在参考平面上的方向就是+x-轴。相关条目春分点昼夜平分点轨道交点

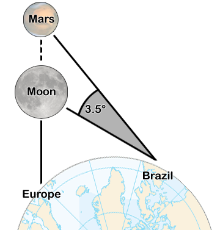
历史亚美利哥·韦斯普奇确定经度的方法对于地图绘制和远洋航海来说，经度的测量是很重要的。在历史上的大多数时候，水手和探险家们为了确定经度而绞尽脑汁。人们花费了几个世纪来探索确定经度的方法，因此，经度的历史记录了一些最伟大的科学头脑的努力。使用四分仪或星盘可观测到太阳或某特定恒星在地平线上的高度，根据该高度可以计算出该位置的纬度，但是经度的确定要更加复杂些。亚美利哥·韦斯普奇（AmerigoVespucci，1454/03/09－1512/02/22）也许是第一个提出经度确定方法的欧洲人，他在前往新世界的旅途中，花费了大量的时间和精力来研究这个问题：约翰·哈里森通过对比月球和火星的实际位置与它们的预期位置，亚美利哥·韦斯普奇得以初步推测出他的经度位置。但是他的方法有几点局限：第一，此方法要求发生一些特殊的天文现象(比如，火星和月球穿越相同的升交点赤经)，并且要求观测者通过天文历书预测到这种现象...

幸得沉香，尤获至宝。我亦喜静，烟云人生。香道讲究静观不语，需要人们随着袅袅升起的轻烟静静地感悟其中的人生道理。一缕青烟从半明半灭的微光中徐徐飘出，渐渐消散在空气中。淡雅的香气丝丝缕缕窜入鼻中，香味在空气中筑起一块清静之地，任外界喧嚣，只沉浸在自己的世界里。源于物质，散于精神。品茗焚香，宁静致远。静看烟云，人海浮沉。熙熙攘攘，幸能心安。不少人听说香，就以为是宗教用的香，其实它只是香学中很小的范畴。中国人用香的历史可说是非常的早，中国用香的文明可概括为：肇始于春秋战国，滋长于秦汉两朝，完备于隋唐五代，鼎盛于宋元明清。宋代陈去非的诗作在一定程度上代表了中国古代文人对香的态度：明窗延静书，默坐消尘缘;即将无限意，寓此一炷烟。当时戒定慧，妙供均人天;我岂不清友，于今心醒然。炉烟袅孤碧，云缕霏数千;悠然凌空去，缥缈随风还。世事有过现，熏性无变迁;应是水中月，波定还自圆。从宋代起，出现了各种香材研磨混合...

导读：英国格林尼治天文台最早建于1676年。它成为全世界最负盛名的天文台的重要原因之一是，人们在这里找到了世界通用的“经度”。格林尼治天文台第一个研究出了简易测定航海中船舶方位的方法。测定位置需要两个参数：经度和纬度。海员们很早就懂得在夜间比照北斗星的高度角推算纬度，可是经度的计算要难得多。精确的海图出现之前，航海家只能用罗盘、铅垂线或大致估计的船速来确定自己的地理位置，很不可靠。因此，在15世纪航海事业走向常规化的时候，随时测定船舶的位置就成了一个迫在眉睫的问题，也成了当时欧洲各国科学家竞技的焦点。格林尼治天文台最初的使命是：观测星空，绘制完整的星空图。这样人们就可以按照星空图来测定船舶所在地的经度。但这是一个费时费力、需要大量专业人才和专业观测工具与地点的工作。星空图绘制工作还没有完成的问题在18世纪初终于从“不便”演变成了“灾难”。1707年10月，4艘英国海军的船只因为定位混乱而在...

计算在太空动力学，近心点幅角ωω-->{\displaystyle\omega\,}可由下式计算：此处：n{\displaystyle\mathbf{n}}是指向昇交点的向量（此处是z-分量n{\displaystyle\mathbf{n}}为0），e{\displaystyle\mathbf{e}}是离心向量（指向近心点的方向）。在赤道轨道上，无须精确的定义此一参数，他经常被假设如下：此处：ex{\displaystylee_{x}\,}是离心向量的x-分量e{\displaystyle\mathbf{e}\,}在原轨道的情况下，经常会假设近心点就在昇交点的方向下，也就是ωω-->=0{\displaystyle\omega=0\,}。