向量分析

大致来说，向量分析中的曲线积分可以看成在某一场中沿特定路径的累积效果。更具体地说，如果曲线C⊆ ⊆ -->R2{\displaystyle C\subseteq \mathbb {R} ^{2}}，标量场的曲线积分可以想成某个曲线（不是C{\textstyle C}）向下切割出的面积，这可以通过建立函数z = f(x,y)和x-y平面内的曲线C来想像这个曲面，可以把x-y{\displaystyle x{\text{-}}y}平面上的曲线C{\displaystyle C}想成屏风的底座，f{\displaystyle f}代表在该点屏风的高度（这里假设f≥ ≥ -->0{\displaystyle f\geq 0}），则f{\displaystyle f}的曲线积分就是该“屏风”的面积，也就是前面所说曲线(x(t),y(t),f(x,y)){\textstyle (x(t),y(t),f(x,y))}向下切割的面积，其中(x(t),y(t)){\textstyle (x(t),y(t))}是曲线C{\textstyle C}的参数化。

标量场的曲线积分

梯度场中的曲线积分

定义

设有标量场：F : U ⊆ R→ → -->{\displaystyle \to }R，则对于路径C ⊂ U，F的曲线积分是：

其中，r: [a, b] → → -->{\displaystyle \to }C 是一个一一对应的参数方程，并且r(a)和r(b)分别是路径曲线C的两个端点。

f称为积分函数，C是积分路径。不严格地说，ds可以被看作积分路径上的一段很小的“弧长”。曲线积分的结果不依赖于参量化函数r。

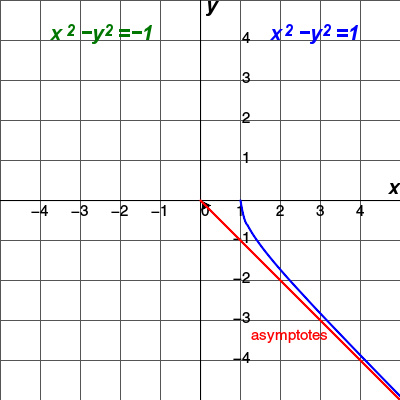
几何上，当标量场f定义在一个平面（n=2）上时，它的图像是空间中一个曲面z=f(x,y)，曲线积分就是以曲线C为界的有符号的截面面积。参见动画演示。

推导

对于标量场上的曲线积分，

向量场的曲线积分

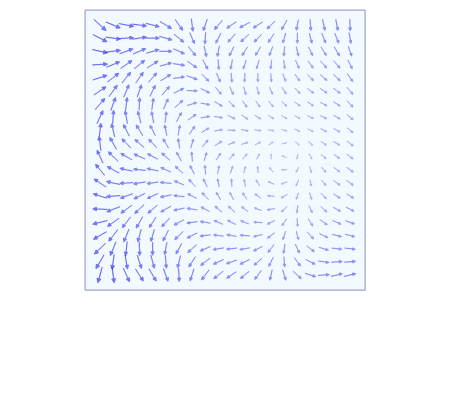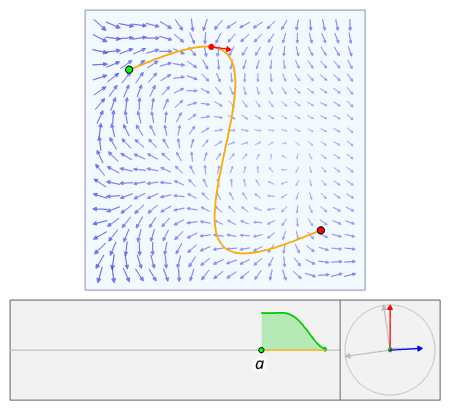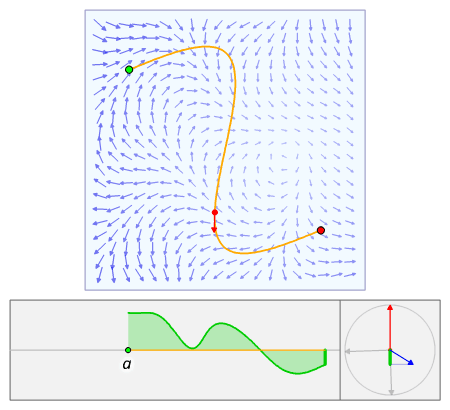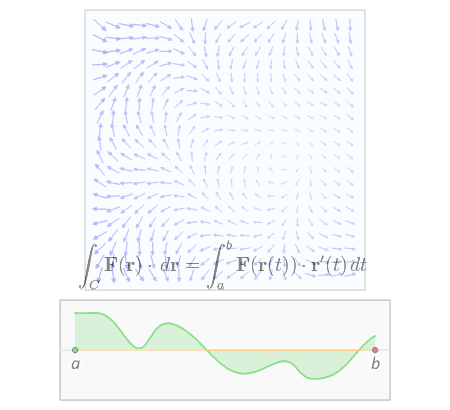
向量场的曲线积分

设有向量场：F : U ⊆ R→ → -->{\displaystyle \to }R，则其在路径C ⊂ U上关于方向r的曲线积分是：

其中，r: [a, b] → → -->{\displaystyle \to }C 是一个一一的参量化函数，并且r(a)和r(b)分别是路径曲线C的两个端点。这时曲线积绝对值绝对值与参量化函数r无关，但其方向与参量化函数r的选择有关。特别地，当方向相反时，积分值也相反。

与路径无关的条件

如果向量场F是一个标量场G的梯度，即：

那么，由G和r组成的复合函数的导数是：

于是对路径C就有：

用文字表示，就是说若F是一个梯度场，那么F的曲线积分与所取的路径无关，而只与路径的起点和终点的选取有关。

应用

在各种保守力的场都是路径无关的，一个常见的例子就是重力场或电场。在计算这种场的做功时，可以选择适当的路径进行积分，使得计算变得简单。

曲线积分与复分析的关系

如果将复数看作二维的向量，那么二维向量场的曲线积分就是相应复函数的共轭函数在同样路径上的积分值的实部。

根据柯西-黎曼方程，一个全纯函数的共轭函数所对应的向量场的旋度是0。

复曲线积分

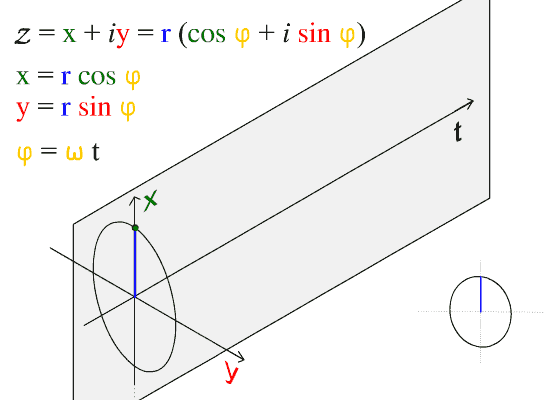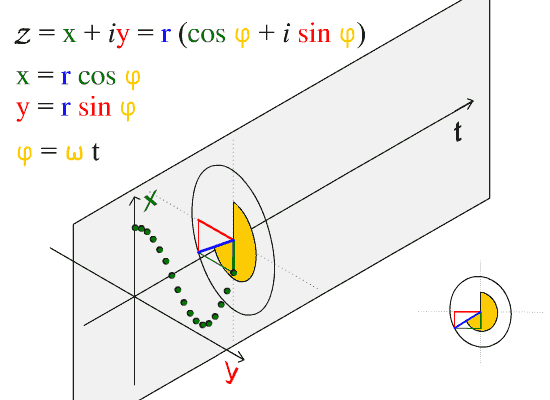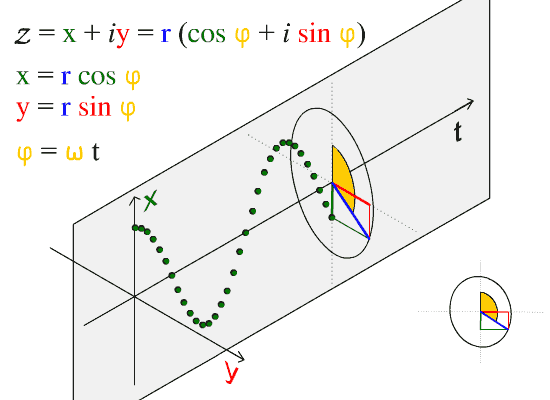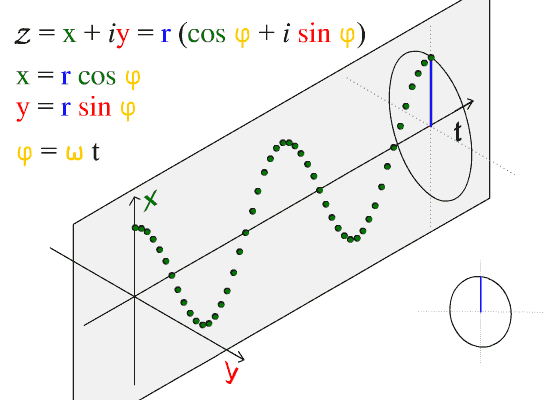
在复分析中，曲线积分是通过复数的加法和乘法定义的。令U为复数集C 的一个开子集，f : U→ → -->{\displaystyle \to }C是一个函数，L⊂ ⊂ -->U{\displaystyle L\subset U}是一个参数为γ γ -->:[a,b]→ → -->L{\displaystyle \gamma :[a,b]\to L}的可求长曲线，其中γ γ -->(t)=x(t)+iy(t).{\displaystyle \gamma (t)=x(t)+iy(t).}。则曲线积分：

可以通过将区间[a, b]分划为a = t0 < t1 < ... < tn = b来定义。考虑下式：

曲线积分是区间分划的长度趋于零时这个黎曼和的极限。

当γ γ -->{\displaystyle \gamma }连续可微时，曲线积分可以用一个实变函数的积分表示：

当L{\displaystyle L}为闭合曲线时，积分的起点和终点重合，这时f沿L{\displaystyle L}的曲线积分通常记作

对于共轭微分算子dz¯ ¯ -->{\displaystyle {\overline {dz}}}的曲线积分定义为

复函数的曲线积分有很多技巧。将复函数分作实部和虚部，可以将问题简化为两个实值函数的曲线积分。其它情况下可以用柯西积分公式。如果积分路径是闭合的，并且积分函数在区域中是解析的且没有奇点，那么它的曲线积分是零，这是柯西积分定理的推论。根据留数定理，可以用复平面上的围道积分计算实质函数在实区间上的积分。

例子

考虑复函数f(z)=1/z，设积分路径L为单位圆（模长为1的复数的集合）。我们使用γ(t)=e来将路径参数化，其中t在[0, 2π]内。代入积分式就得到：

∮Lf(z)dz=∫ ∫ -->02π π -->1eitieitdt=i∫ ∫ -->02π π -->e− − -->iteitdt=i∫ ∫ -->02π π -->dt=i(2π π -->− − -->0)=2π π -->i.{\displaystyle {\begin{aligned}\oint _{L}f(z)\,dz&=\int _{0}^{2\pi }{1 \over e^{it}}ie^{it}\,dt=i\int _{0}^{2\pi }e^{-it}e^{it}\,dt\\&=i\int _{0}^{2\pi }\,dt=i(2\pi -0)=2\pi i.\end{aligned}}}

用柯西积分定理也可以得到结果。

量子力学

量子力学中的“曲线积分形式”和曲线积分并不相同，因为曲线积分形式中所用的积分是函数空间上的泛函积分，即关于空间中每个路径的概率函数进行积分。然而，曲线积分在量子力学中仍有重要作用，比如说复围道积分常常用来计算量子散射理论中的概率振幅。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。