算法

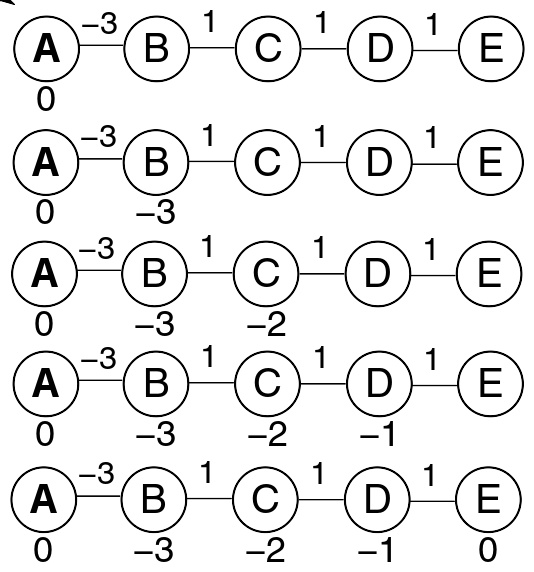
在这个图中，假设A是起点，并且边以最坏的顺序处理，从右到左，需要|V|−1步或4次计算路径长度。相反地，若边以最优顺序处理，从左到右，算法只需要在一次遍历内完成。

贝尔曼-福特算法与迪科斯彻算法类似，都以松弛操作为基础，即估计的最短路径值渐渐地被更加准确的值替代，直至得到最优解。在两个算法中，计算时每个边之间的估计距离值都比真实值大，并且被新找到路径的最小长度替代。 然而，迪科斯彻算法以贪心法选取未被处理的具有最小权值的节点，然后对其的出边进行松弛操作；而贝尔曼-福特算法简单地对所有边进行松弛操作，共| V | − 1次，其中 | V |是图的点的数量。在重复地计算中，已计算得到正确的距离的边的数量不断增加，直到所有边都计算得到了正确的路径。这样的策略使得贝尔曼-福特算法比迪科斯彻算法适用于更多种类的输入。

贝尔曼-福特算法的最多运行O（| V |·| E |)次，| V |和| E |分别是节点和边的数量）。

伪代码表示

原理

松弛

每次松弛操作实际上是对相邻节点的访问，第 n {\displaystyle n} 次松弛操作保证了所有深度为n的路径最短。由于图的最短路径最长不会经过超过 V − − --> 1 {\displaystyle V-1} 条边，所以可知贝尔曼-福特算法所得为最短路径。

负边权操作

与迪科斯彻算法不同的是，迪科斯彻算法的基本操作“拓展”是在深度上寻路，而“松弛”操作则是在广度上寻路，这就确定了贝尔曼-福特算法可以对负边进行操作而不会影响结果。

负权环判定

因为负权环可以无限制的降低总花费，所以如果发现第 n {\displaystyle n} 次操作仍可降低花销，就一定存在负权环。

优化

循环的提前跳出

在实际操作中，贝尔曼-福特算法经常会在未达到V-1次前就出解，V-1其实是最大值。于是可以在循环中设置判定，在某次循环不再进行松弛时，直接退出循环，进行负权环判定。

队列优化

求单源最短路的SPFA算法的全称是：Shortest Path Faster Algorithm。 SPFA算法是西南交通大学段凡丁于1994年发表的。 松弛操作必定只会发生在最短路径前导节点松弛成功过的节点上，用一个队列记录松弛过的节点，可以避免了冗余计算。复杂度可以降低到O(kE)，k是个比较小的系数(并且在绝大多数的图中，k<=2，然而在一些精心构造的图中可能会上升到很高)

Begininitialize-single-source(G,s);initialize-queue(Q);enqueue(Q,s);whilenotempty(Q)dobeginu:=dequeue(Q);foreachv∈adj[u]dobegintmp:=d[v];relax(u,v);if(tmpd[v])and(notvinQ)thenenqueue(Q,v);end;end;End;

样例

例：V={v1,v2,v3,v4} E={(v1,v2),(v1,v3),(v2,v4),(v4,v3)} weight(v1,v2)=-1 weight(v1,v3)=3 weight(v2,v4)=3 weight(v4,v3)=-1

运行如表： D:Dist[v]，P:Pred[v]

参考文献

^

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。