相关名称

基本定义

真值表定义

A与B 的真值表（也写作 A ∧ ∧ --> {\displaystyle \land } B （逻辑学）， A && B （计算机科学），或 A ⋅ ⋅ --> {\displaystyle \cdot } B （电子学））。

A ∧ ∧ --> B {\displaystyle ~A\land B} 的真值表:

推理规则

合取引入规则 （∧+）（conjunction introduction rule）：

形式化为：

例如:

合取消去规则 （∧-）（Conjunction elimination rule）：

或者,

形式化为:

或者,

合成与分解规则

作为一种推理规则，联言推理的合成式是经典逻辑中简单且有效的论证形式。这个论证形式有两个前提， A 和 B ，可以直观地推出他们的合取。

用逻辑运算符写作：

下面的例子是一个满足联言推理的合成式的论证：

联言推理的分解式是另一个在经典逻辑中简单且有效的论证形式。从任何合取式中都可以直观地推论出两个前提中的任意一个。

...或者，

用逻辑运算符描述为，

...或者

性质

逻辑与满足以下性质：

结合律: A ∧ ∧ --> ( B ∧ ∧ --> C ) ≡ ≡ --> ( A ∧ ∧ --> B ) ∧ ∧ --> C {\displaystyle A\land (B\land C)\equiv (A\land B)\land C}

交换律: A ∧ ∧ --> B ≡ ≡ --> B ∧ ∧ --> A {\displaystyle A\land B\equiv B\land A}

分配律: ( A ∧ ∧ --> ( B ∨ ∨ --> C ) ) ≡ ≡ --> ( ( A ∧ ∧ --> B ) ∨ ∨ --> ( A ∧ ∧ --> C ) ) {\displaystyle (A\land (B\lor C))\equiv ((A\land B)\lor (A\land C))}

幂等律: A ∧ ∧ --> A ≡ ≡ --> A {\displaystyle A\land A\equiv A}

单调性: ( A → → --> B ) → → --> ( ( C ∧ ∧ --> A ) → → --> ( C ∧ ∧ --> B ) ) {\displaystyle (A\rightarrow B)\rightarrow ((C\land A)\rightarrow (C\land B))}

保真性 : 所有变量的真值皆为“真”的命题在逻辑与运算后的结果为真。

保假性 : 所有变量的真值皆为“假”的命题在逻辑与运算后的结果为假。

如果用二进制来表达真（1）和假（0），逻辑与运算与算术乘法运算一致。

计算机科学中的运用

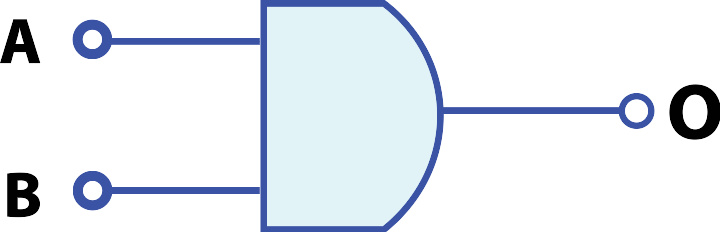
与门

位运算

逻辑与常在位运算中使用，比如：

0 and 0 = 0

0 and 1 = 0

1 and 0 = 0

1 and 1 = 1

1100 and 1010 = 1000

编程中的使用

在高等计算机编程中，逻辑合取“与”通常由内置算符and或&号来表达。很多编程语言还提供与逻辑与相应的短路求值控制结构。

布尔“与”也在SQL的运算符中使用。有些数据库区分大小写，需要"AND"符号。

在计算机科学中，AND运算符可以用来构造位屏蔽，以选择二进制序列的一部分。比如 1001 1 101 AND 0000 1 000 = 0000 1 000 用来取二进制序列的第五位。

交集运算

集合论中的交运算是用逻辑与来定义的： x ∈ A ∩ B 当且仅当( x ∈ A ) ∧ ( x ∈ B )。因此逻辑与有很多与交集运算相同的性质，诸如结合律，交换律，分配律，及德·摩根定律。

参见

与门

相关网页

Wolfram Mathematics Conjunction

All Math Words Encyclopedia Conjunction

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。