实验装置

斐索实验用到的仪器

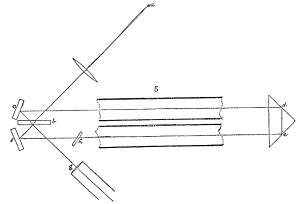
从光源 S′ 放出的光线在被分光镜 G 反射后经透镜 L 准直为两束平行光。两束光线在通过狭缝 O 1 和 O 2 后进入管道 A 1 和 A 2 。两个管道分别按照箭头所指的方向通入水流。在透镜 L′ 焦点处放置的平面镜 m 是为了确保两束光中有一束总顺着水流方向传播，而另一束则逆着水流传播。在通过水管后，两束光线会在 S 处会聚形成干涉条纹。干涉条纹可以用来分析水管中的光速。

菲涅耳拖拽系数

假设管中水流速度为 v 。依据非相对论性理论，光速在以太被水“拖拽”时增大，而在以太“克服”水阻力时减小。总光速是光与水的相对速度与水速的和。

当 n 是水的折射率时，静水中的光速会是 c/n 。那么上述实验中，沿着水流方向传播的光的速度是

逆着水流方向传播的光的速度则会是

也就是说逆着水流传播的光会比顺着水流传播的光速度慢。

观察者看到的两束光重新会聚形成的干涉条纹取决于两束光的光程差。它可以用来确定光速与水速之间的函数关系。

斐索发现

也就是说，光确实受到水的拖拽效应的影响，但拖拽效应却比预期弱很多。

斐索实验令物理学家接受了奥古斯丁·菲涅耳1818年提出的以太部分拖拽理论。菲涅耳曾利用此理论解释弗朗索瓦·阿拉戈1810年做的一项的实验的结果。依据这种理论，光速由介质拖拽效应产生的增加量只是介质速度的一部分，拖拽系数 f 满足

1895年，亨德里克·洛伦兹又在其中加入了与色散有关的项：

重复实验

迈克耳孙与莫雷1886改进的仪器。准直光从光源 a 射向分光镜 b 。其中一束沿着 b c d e f b g 路径传播，另一束则沿着 b f e d c b g 路径传播。

阿尔伯特·迈克耳孙与爱德华·莫雷1886年重复了斐索的实验，并提升了精度。他们认为斐索的原始实验存在以下问题：

仪器变形会导致干涉条纹失真；

由于加压水流持续时间很短，观察时间非常有限；

层流效应导致只有水流最中心部分的流速符合要求，这会导致条纹模糊；

斐索测定的水速也存在不确定度。

迈克耳孙重新设计了实验仪器。他加大了管径并使用了一个可以提供三分钟稳定水流的大水池。他所设计的同光路干涉仪（ common path interferometer ）可以自动补偿光路长度。结构上说，光路与萨尼亚克干涉仪（ Sagnac interferometer ）中的相同。每条光路上都会产生偶数次反射。 这种仪器对于一阶效应的稳定性非常高，并且对于其中任何组件的移位都不敏感。即使在 h 处放一个玻璃盘或者在光路中放入一个点燃的火柴也不会使条纹中心发生偏移。迈克耳孙与莫雷利用这种仪器确认了斐索的结果。

彼得·塞曼也在1914年到1915年间做了重复实验。他将迈克耳孙的仪器的规模进一步扩大，并将其仪器直接与阿姆斯特丹的主供水管道相连。塞曼还对波长在 4,358 Å （紫）到 6,870 Å （红）范围内的单色光也进行了测量，以验证洛伦兹修改后的系数。 1910年，弗朗茨·哈雷斯（ Franz Harress ）使用了可以旋转的仪器来确认菲涅耳拖拽系数。不过，他发现数据存在“系统性的偏差”。后来他发现这是由 萨尼亚克效应 （ 英语 ： Sagnac effect ） 造成的。 从那时起，许多测量拖拽系数的结果也都伴有萨尼亚克效应的影响。 比如，使用转盘与 环形激光 （ 英语 ： ring laser ） 的实验 或者 中子干涉 （ 英语 ： Neutron interferometer ） 实验。 此外，相关研究人员还发现了垂直于光运动的介质产生的横向拖拽效应。

赫克实验

马丁·赫克 （ 英语 ： Martin Hoek ） 也在1868年间接验证了菲涅耳系数。 他所用的实验装置与斐索的类似，不过其中一条干涉臂充入的是静水，另一条则是空气。在静止以太中的观察者看来，地球是运动的，也就是说上述装置中的水也是运动的。所以两束传播方向相反的光的传播时间为（忽略横向效应）：

在上图所展示的实验中，赫克先让狭缝透过的光经棱镜 P 色散，然后经 C 准直再进入主体装置。他预测当仪器朝向与以太风平行时，一条回路中的光会受到以太风的影响相对于另一条回路发生7/600mm的偏移。当这个偏移是光谱中某些光波长的整数倍时就会产生亮条纹；当偏移是波长半整数倍时就会产生暗条纹。而在仪器朝向与以太风垂直时，赫克预测看到的应是连续谱。而在实际实验中，无论仪器朝向如何，他却都没有看到条纹。赫克原本预测，两束光的传播是时间并不相同，因此应该能看到干涉偏移。然而，如果对以太系中的水适用菲涅耳拖拽系数，这种时间差（ v/c 一阶效应）就会消失。赫克在使用不同的装置时得到的也是零结果。这也就验证了菲涅耳拖拽系数。（ 古斯塔夫·哈马尔 （ 英语 ： Gustaf Wilhelm Hammar ） 也曾进行过 类似的实验 （ 英语 ： Hammar experiment ） 。该实验否定了以太风存在的可能性。）

争议

尽管菲涅耳假说可以解释斐索的实验结果，但在这个领域的专家看来，包括斐索本人（1851）、 埃勒泰尔·马斯卡尔 （ 英语 ： Éleuthère Mascart ） （1872）、克特勒（1873）、费尔特曼（1873）以及洛伦兹（1886），菲涅耳的以太部分拖拽假说并不可靠。比如，费尔特曼1870年提出对于不同波长的光，对应的拖拽系数并不相同，因为不同色光的折射率不同。马斯卡尔则在1872年测定双折射介质中偏振光的情况时也得到了类似结果。换言之，以太要同时有两种不同的拖拽系数。

斐索本人在实验报告的结论中也表达了不满：

尽管这些物理学家都对菲涅耳的以太部分拖拽假说表示不满，但这种假说还是得到了其他科学家在更高精度下的验证。（见上文）

以太部分拖拽假说除了本身有问题之外，还与迈克耳孙-莫雷实验（1887）的结果并不兼容。在菲涅耳的假说里，以太几乎绝对静止，所以通过迈克尔孙-莫雷实验应该能得到以太存在的证据。但迈克尔孙-莫雷实验的结果表明绝对静止的以太不可能存在。从以太模型的角度来说，当时的实验结果之间存在很大的分野：一方面，光行差、斐索实验以及后续重复实验支持“以太部分拖拽模型”；另一方面，迈克耳孙-莫雷实验则支持以太相对于地球完全静止的“完全以太拖拽模型”。 由此引起的理论危机直到狭义相对论出现后才得到解决。

洛伦兹的解释

1892年，亨德里克·洛伦兹对于菲涅耳的模型做了修正。在他的模型中，以太是完全静止的。洛伦兹利用水与静止以太之间的相互作用推出了菲涅耳拖拽系数。 他还发现可以通过引入时间参量，“局部时”，来简化参考系之间的变换：

1895年，洛伦兹基于局部时的概念给出了菲涅耳系数更为普遍的解释。然而，洛伦兹的理论与菲涅耳的理论具有相同的基础问题，即不能与迈克耳孙-莫雷实验的结果相调和。所以洛伦兹在1892年提出了运动物体会在运动方向上发生长度收缩的假说（乔治·斐兹杰惹也在1889年提出类似假说）。他后来又继续发展能够描述这些效应的方程。最终的方程组后来叫做“洛伦兹变换”。这个方程组与爱因斯坦后来从第一性原理推得的方程组形式相同。但与爱因斯坦的方程组不同的是，洛伦兹的方程组只是特例假设，也就是说它们只是为了使已有的理论成立才设立的。

狭义相对论解释

爱因斯坦后来展示了洛伦兹的方程组如何从狭义相对论的两条公设推出。除此之外，爱因斯坦还认定静止以太在狭义相对论中没有存在的必要，并且洛伦兹变换与时空本身性质有关。与移动中的磁铁与导体问题、以太零漂移实验以及光行差问题一样，斐索实验是促成爱因斯坦形成相对性思想的关键实验结果之一。 罗伯特·尚克兰 （ 英语 ： Robert S. Shankland ） 与爱因斯坦曾经有过几次交流。爱因斯坦是这样强调斐索实验的重要性的：

马克斯·冯·劳厄在1907年展示了菲涅耳拖拽系数可以通过相对论中的速度加成式推出：

斐索实验也因此可以验证爱因斯坦速度加成式在合成速度共线的情况下成立。

参看

狭义相对论的实验验证

狭义相对论发现史

参考文献

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。