前向、后向与混合稳定性

在数值线性代数中经常使用前向、后向以及混合稳定性的概念。

该图显示了前向误差Δy、后向误差Δx、它们与精确解f以及数值解f* 的关系

假设要用数值算法解决的问题是用函数f将数据x映射到解y，通常算法的结果y* 会与“真”解y有一定的偏差。误差的来源主要有舍入误差、截断误差以及数据误差。算法的前向误差是结果与真解之间的差别，在这里是Δy = y* − y。后向误差是满足f(x + Δx) = y* 的最小Δx，也就是说后向误差说明算法的所解决的问题。前向误差和后向误差通过条件数发生关系：前向误差的幅度最多是条件数乘以后向误差的幅度。

在许多情况下，需要考虑相对误差

而不是绝对误差Δx。

如果对于任意的输入x来说后向误差都很小，那么算法就是后向稳定的。当然，“小”是一个相对的概念，需要根据所用的场合进行定义。通常要求误差要与单位舍入误差处于同一数量级。

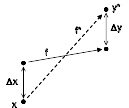
包括前向误差与后向误差概念的混合稳定性

通常数值稳定性的定义是使用一个包括了前向误差与后向误差的更加宽泛的概念，称为混合稳定性。按照这个概念，如果一个算法是稳定的，那么存在Δx使得Δx与f(x + Δx) − y* 都很小。因此，后向稳定算法永远是稳定的。

如果算法的前向误差除以条件数得到的结果很小，那么这个算法就是前向稳定的。这就意味着如果一个算法的前向误差与后向稳定算法的误差幅度类似那么就是前向稳定的。

数值微分方程的稳定性

上面的定义在截断误差不重要的情况下是很确切的。在微分方程等另外一些场合中，则需要另外的数值稳定性定义。

在数值常微分方程中，有不同的数值稳定性概念，如A稳定性等。它们通常与动力系统中的李雅普诺夫稳定性等稳定性概念相关。在解刚度方程的时候稳定方法的使用很重要。

在数值偏微分方程中另外一种数值稳定性的定义。如果随着步长逐渐趋近于零，偏微分方程的数值解仍然保持有界，那么这个算法就是稳定的。拉克斯等价定理表明如果算法是一致稳定的，那么这个算法就会收敛。有时候将数值扩散考虑在内来实现稳定性。数值扩散是一个数学术语，它保证舍入误差以及其它误差在计算的过程中逐渐散去，而不会累积起来越变越大。

参考文献

Nicholas J. Higham, Accuracy and Stability of Numerical Algorithms, Society of Industrial and Applied Mathematics, Philadelphia, 1996. ISBN 0-89871-355-2.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。