定义

File:Topological vector space illust2.svg 如果乘法运算在 0 处是连续的，则对于 0 的任何邻域 U 和任何标量 λ 存在另一个 0 的邻域 V 使得 λ V 被包含在 U 中。这个必要条件也会变为充分条件，如果增加了额外假设；参见Trèves (1967， Chapter 3)。

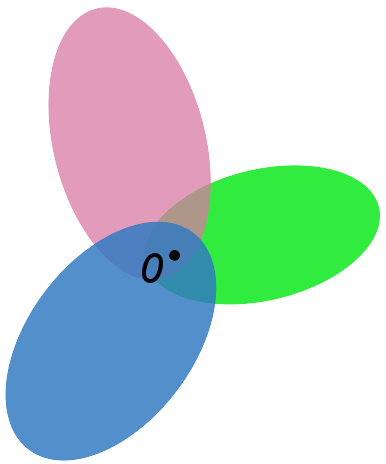
带有上述两个性质的原点的邻域族唯一确定一个拓扑向量空间。在这个向量空间内的任何其他点的邻域系统是通过平移获得的。

一个 拓扑向量空间 X 是布于一个拓扑域 K （通常取实数或复数域）上的向量空间，其上带有拓扑结构使得向量加法 X × X → X 与标量乘法 K × X → X 为连续映射。

注 ：某些作者也要求 X 是豪斯多夫空间，更有要求其为局部凸空间者（例如 Fréchet 空间）。一个拓扑向量空间是豪斯多夫空间的充分条件是该空间为 T 1 {\displaystyle T_{1}} 空间。

布于 K 上的拓扑向量空间范畴通常记为 TVS K 或 TVect K ，其对象为布于 K 上的拓扑向量空间，态射则为连续的 K -线性映射。拓扑向量空间的同构是既是同胚也是线性的映射。

例子

所有赋范向量空间都是拓扑向量空间的例子。因此所有巴拿赫空间及希尔伯特空间也是这些例子。

函数空间

更多资料：函数空间

在数学分析中应用的拓扑向量空间主要是函数空间。较常见的例子有：

C ( X ) {\displaystyle C(X)} ：拓扑空间 X {\displaystyle X} 上的连续函数空间，其拓扑由一族半范数 ∥ ∥ --> f ∥ ∥ --> := sup x ∈ ∈ --> K | f ( x ) | {\displaystyle \|f\|:=\sup _{x\in K}|f(x)|} 定义，其中 K {\displaystyle K} 遍取 X {\displaystyle X} 中的紧子集。

C 0 ( X ) {\displaystyle C_{0}(X)} ：拓扑空间 X {\displaystyle X} 上的紧支撑集连续函数空间，拓扑由范数 ∥ ∥ --> f ∥ ∥ --> := sup | f ( x ) | {\displaystyle \|f\|:=\sup |f(x)|} 定义。

Lp空间：测度空间 ( X , μ μ --> ) {\displaystyle (X,\mu )} 上满足 ∫ ∫ --> | f | p d μ μ --> {\displaystyle \int |f|^{p}\mathrm {d} \mu 的函数空间，拓扑由范数 ∥ ∥ --> f ∥ ∥ --> p := ( ∫ ∫ --> | f | p d μ μ --> ) 1 / p {\displaystyle \|f\|_{p}:=(\int |f|^{p}\mathrm {d} \mu 定义，其中 p ∈ ∈ --> [ 1 , + ∞ ∞ --> ] {\displaystyle p\in [1,+\infty ]}

索伯列夫空间：偏微分方程理论中常用的空间，详见主条目索伯列夫空间。

分布：一种广义函数理论，用以定义并研究偏微分方程的广。全体分布构成一个拓扑向量空间。

施瓦兹空间：又称快速递减函数空间，定义为 S ( R n ) := { f ∈ ∈ --> C ∞ ∞ --> ( R n ) ∣ ∣ --> | | f | | α α --> , β β --> ∀ ∀ --> α α --> , β β --> } {\displaystyle {\mathcal {S}}\left(\mathbb {R} ^{n}\right):=\{f\in C^{\infty }(\mathbb {R} ^{n})\mid ||f||_{\alpha ,\beta } ，其中 α α --> , β β --> {\displaystyle \alpha ,\beta } 为多重指标，其中的半范数由 | | f | | α α --> , β β --> = | | x α α --> D β β --> f | | ∞ ∞ --> {\displaystyle ||f||_{\alpha ,\beta }=||x^{\alpha }D^{\beta }f||_{\infty }} 给出。此空间的重要性主要在于傅立叶变换理论。

积向量空间

当赋予乘积空间后，拓扑向量空间的家族的笛卡儿乘积都是拓扑向量空间．例如， X 是 f : R → R 函数的集合. X 可以被乘积空间 R 来确定的，并带有自然的乘积空间．有了这个拓扑， X 成了拓扑向量空间，称呼为逐点收敛的空间．命名的原因是如果( f n ) 是 X 集合内元素的序列而对于所有实数 x f n ( x )都有一个极限 f ( x ) ，那么 f n 在 X 集合内有一个极限 f ．这个空间就是完整但不能赋范．

拓扑结构

向量空间对加法构成阿贝尔群，拓扑向量空间的加法逆运算 v ↦ ↦ --> − − --> v {\displaystyle v\mapsto -v} 是连续的（因为 − − --> v = ( − − --> 1 ) ⋅ ⋅ --> v {\displaystyle -v=(-1)\cdot v} ），拓扑群扑向量空间可视为可交换的拓扑群。

特别是：拓扑向量空间是一致空间，因此可以谈论完备性、一致收敛与一致连续。向量运算（加法与标量积）是一致连续的，因此拓扑向量空间的完备化仍为拓扑向量空间，原空间在其中是个稠密的线性子空间。

向量运算不只连续，实则还是同胚，因此我们可以从原点附近的一组局部基重构整个空间的拓扑。局部基可由以下两种开集组成：

吸收集： ∀ ∀ --> v ∈ ∈ --> E ∃ ∃ --> α α --> ∈ ∈ --> R + ∗ ∗ --> ∀ ∀ --> λ λ --> ∈ ∈ --> K | λ λ --> | ≤ ≤ --> α α --> ⇒ ⇒ --> λ λ --> v ∈ ∈ --> U {\displaystyle \forall v\in E\quad \exists \alpha \in \mathbb {R} _{+}^{*}\quad \forall \lambda \in K\quad |\lambda |\leq \alpha \Rightarrow \lambda v\in U} ；事实上，原点的任何邻域都是吸收集。

平衡集： ∀ ∀ --> λ λ --> ∈ ∈ --> K ∀ ∀ --> v ∈ ∈ --> E | λ λ --> | ≤ ≤ --> 1 ⇒ ⇒ --> λ λ --> v ∈ ∈ --> U {\displaystyle \forall \lambda \in K\quad \forall v\in E\quad |\lambda |\leq 1\Rightarrow \lambda v\in U}

一个拓扑向量空间可度量化的充要条件是：（一）它是豪斯多夫空间（二）原点有一组可数的局部基。

拓扑向量空间之间的线性函数若在某一点连续，则在整个定义域上连续。一个线性泛函连续的充要条件是其核为闭子空间。

有限维向量空间有唯一的豪斯多夫拓扑，因此任何有限维拓扑向量空间都同构于 K n {\displaystyle K^{n}} （带上确界范数： ∥ ∥ --> ( a 1 , … … --> , a n ) ∥ ∥ --> := sup | a i | {\displaystyle \|(a_{1},\ldots ,a_{n})\|:=\sup |a_{i}|} ）。对于豪斯多夫拓扑向量空间，有限维等价于局部紧。

拓扑向量空间的种类

在应用中，我们常考虑具有一些附带拓扑性质的空间，以下是一些常见的种类，大致以其性质之“良好”与否排序。

局部凸拓扑向量空间：每一点都有一组由凸集构成的局部基。一个空间是局部紧当且仅当其拓扑可由一组半范数定义。局部紧性对某些“几何”论证（例如哈恩-巴拿赫定理）至关重要。

F-空间：由一个具平移不变性的度量定义的完备拓扑向量空间，例子包括Lp空间（p > 0）。

弗雷歇空间：局部凸的 F-空间。许多有趣的函数空间都是弗雷歇空间。

核空间：使得映至任何巴拿赫空间的有界算子均为核算子的弗雷歇空间。

赋范向量空间与半赋范向量空间：顾名思义，即其拓扑由一范数或一族半范数定义的拓扑向量空间。在赋范向量空间中，一算子的连续性等价于有界性。

巴拿赫空间：完备赋范向量空间。泛函分析学大部奠基于此。

自反巴拿赫空间：使得自然映射 V → → --> V ∧ ∧ --> ∧ ∧ --> {\displaystyle V\to V^{\wedge \wedge }} 为同构的巴拿赫空间。非自反空间的重要例子之一是 L 1 {\displaystyle L^{1}} 空间。

希尔伯特空间：拓扑由一内积定义的拓扑向量空间。虽然这类空间可能是无穷维的，大部分有限维上的几何论证仍可照搬至此。

欧几里得空间：即有限维的豪斯多夫拓扑向量空间。

对偶空间

拓扑向量空间 V {\displaystyle V} 的连续对偶空间定义为所有连续线性泛函构成的空间 V ∗ ∗ --> {\displaystyle V^{*}} ，其拓扑可定义为使对偶配对 V ∗ ∗ --> × × --> K V → → --> K : ( λ λ --> , v ) ↦ ↦ --> λ λ --> ( v ) {\displaystyle V^{*}\times _{K}V\to K:(\lambda ,v)\mapsto \lambda (v)} 为连续映射的最粗拓扑（称为弱-*拓扑）。当 V {\displaystyle V} 为巴拿赫空间时， 可以藉算子范数在 V ∗ ∗ --> {\displaystyle V^{*}} 上定义更细的拓扑，然而弱-*拓扑具有一些紧致性定理（巴拿赫-阿劳格鲁定理），因而在应用中仍相当重要。

文献

A Grothendieck: Topological vector spaces , Gordon and Breach Science Publishers, New York, 1973. ISBN 978-0-677-30020-7

G Köthe: Topological vector spaces . Grundlehren der mathematischen Wissenschaften, Band 159, Springer-Verlag, New York, 1969. ISBN 978-0-387-04509-2

Schaefer, Helmuth H. Topological vector spaces. New York: Springer-Verlag. 1971. ISBN 978-0-387-98726-2.

Lang, Serge. Differential manifolds. Reading, Mass.–London–Don Mills, Ont.: Addison-Wesley Publishing Co., Inc. 1972.

F Trèves: Topological Vector Spaces, Distributions, and Kernels , Academic Press, 1967. ISBN 978-0-486-45352-1.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。