数学表示

一般而言，气温垂直递减率可以如此表示：

γ γ -->=− − -->dTdz{\displaystyle \gamma =-{\frac {dT}{dz}}}

γ γ -->{\displaystyle \gamma }为气温垂直递减率，T为温度，z为海拔高度。

注：因为比热比或湿度常数等皆会使用γ γ -->{\displaystyle \gamma }为符号，为了避免混淆，有时会用Γ Γ -->{\displaystyle \Gamma } 或 α α -->{\displaystyle \alpha }代表气温垂直递减率。

种类

气温垂直递减率有两种形式：

环境温度递减率 – 平稳大气下，气温随海拔变化的比率

绝热递减率 – 固定量的空气绝热上升或下降时，气温随海拔变化的比率。绝热递减率有两种：

环境温度递减率

在给定的温度与地点，且大气稳定的情况下，温度随着海拔的变化率称为环境温度递减率。

国际民航组织（ICAO）定义国际标准大气（ISA）从海平面到海拔11km的温度递减率为6.49 K/km。从11km到20km，空气的温度是常数−56.5 °C，是国际标准大气中温度最低的。由于国际标准大气没有将水汽纳入考虑，这个理想化的模型与实际会有误差。比如：在逆温层中，温度反而会随海拔增加。

干绝热直减率

干绝热直减率是一固定分子数的干燥空气，在绝热条件下，温度随海拔高度改变的比率。

给予相同的能量，干燥空气的温度会上升得比潮湿空气快。绝热亦即空气不与外界交换能量。由于空气的导热系数极低，接触传导的热足以忽略，故假设为绝热。

当海拔高度增加时，气压会随之下降，空气体积增加。空气体积增加会推挤其他空气，对其他空气作功。作功的能量来自内能，温度因内能减少而下降。干绝热直减率是9.8 °C/km。

因为是绝热过程：

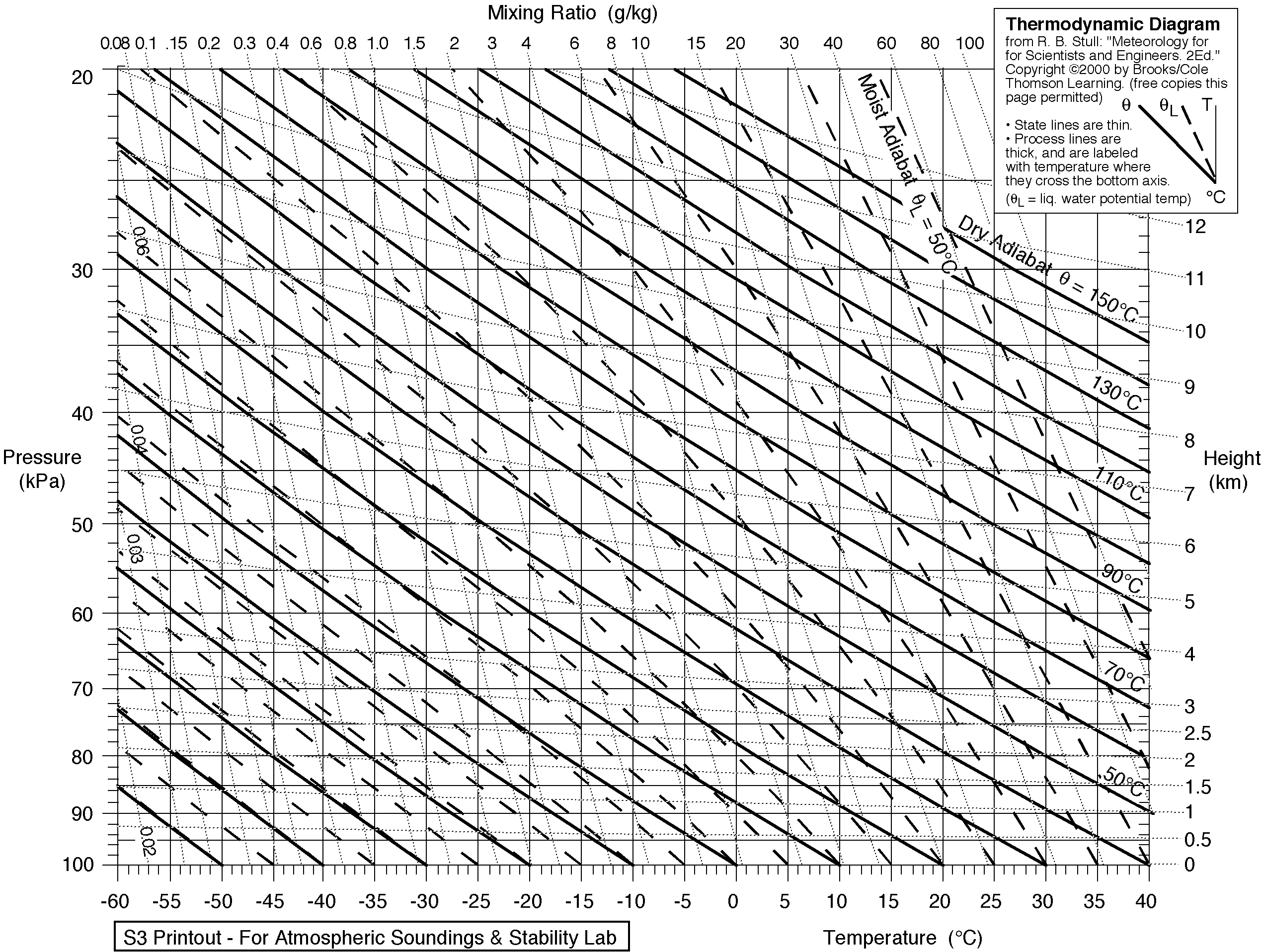
气压温度图，显示干燥绝热线（粗线）和潮湿绝热线（虚线）两者与温度及压力的变化。

PdV=− − -->VdP/γ γ -->{\displaystyle PdV=-VdP/\gamma }

根据热力学第一定律，可以表示成：

mcvdT− − -->Vdp/γ γ -->=0{\displaystyle mc_{v}dT-Vdp/\gamma =0}

又因α α -->=V/m{\displaystyle \alpha =V/m}，且γ γ -->=cp/cv{\displaystyle \gamma =c_{p}/c_{v}}。我们可以将式子表示成：

cpdT− − -->α α -->dP=0{\displaystyle c_{p}dT-\alpha dP=0}

其中，cp{\displaystyle c_{p}}是固定压力下的比热，α α -->{\displaystyle \alpha }是比容。

假设大气处于流体静力平衡：:

dP=− − -->ρ ρ -->gdz{\displaystyle dP=-\rho gdz}

其中，g是标准重力，ρ ρ -->{\displaystyle \rho }是密度。

结合两式，压力可以从式子中消除，解得干绝热直减率：

Γ Γ -->d=− − -->dTdz=gcp=9.8 ∘ ∘ -->C/km{\displaystyle \Gamma _{d}=-{\frac {dT}{dz}}={\frac {g}{c_{p}}}=9.8\ ^{\circ }\mathrm {C} /\mathrm {km} }

饱和绝热直减率

当空气中处于饱和，采用饱和绝热直减率。此比率大约为5 °C/km，受气温的影响很大。

饱和绝热直减率与干绝热直减率之所以相差甚大，是因为水在凝结时会释放潜热，这是雷暴发展的重要能量来源。不饱和空气在给定的气温、海拔与湿度之下上升，此时使用干绝热直减率。随着海拔上升、气温下降，空气达到水汽饱和，采用饱和绝热直减率。

美国气象学会给出的饱和绝热直减率的近似公式：

Γ Γ -->w=g1+HvrRsdTcpd+Hv2rRswT2=g1+HvrRsdTcpd+Hv2rϵ ϵ -->RsdT2{\displaystyle \Gamma _{w}=g\,{\frac {1+{\dfrac {H_{v}\,r}{R_{sd}\,T}}}{c_{pd}+{\dfrac {H_{v}^{2}\,r}{R_{sw}\,T^{2}}}}}=g\,{\frac {1+{\dfrac {H_{v}\,r}{R_{sd}\,T}}}{c_{pd}+{\dfrac {H_{v}^{2}\,r\,\epsilon }{R_{sd}\,T^{2}}}}}}

参见

绝热过程

流体力学

流体动力学

焚风

^Adiabatic Lapse Rate,IUPACGoldbook

^Danielson, Levin, and Abrams, Meteorology, McGraw Hill, 2003

^Landau and Lifshitz, Fluid Mechanics, Pergamon, 1979

^Kittel and Kroemer, Thermal Physics, Freeman, 1980;chapter 6, problem 11

^[1]

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。