



三角波
相关条目正弦波、方波、三角波和锯齿波的波形锯齿波方波参考文献MathWorld上FourierSeries-TriangleWave的资料,作者:埃里克·韦斯坦因。
相关条目
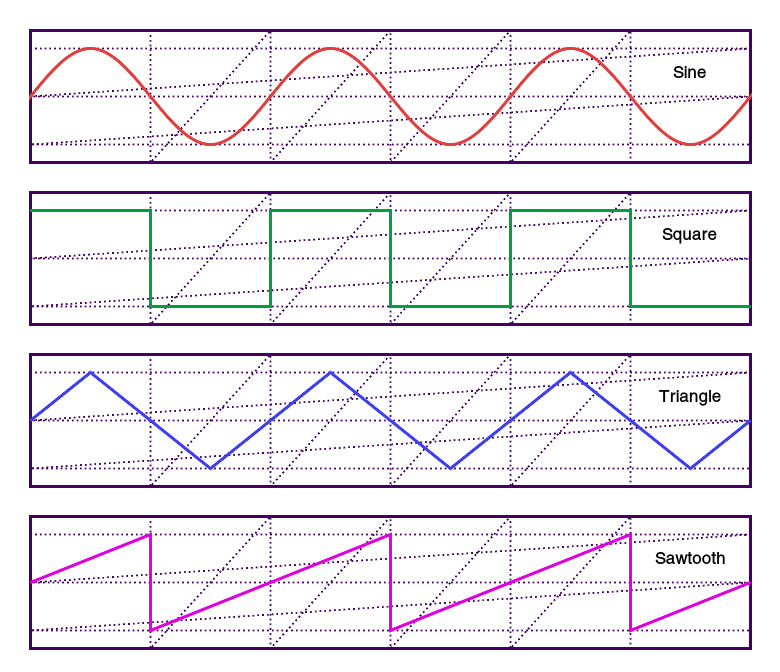
正弦波、方波、三角波和锯齿波的波形
锯齿波
方波
参考文献
MathWorld上Fourier Series - Triangle Wave的资料,作者:埃里克·韦斯坦因。
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 三角战术
运作模式这套战术的需求非常高。第一,需要至少2位身手全面、单打能力出色的球员;第二,场上五人都要具备一定的战术素养;第三,球权平均分配,场上五人都要能投能传。也因为这套战术太过复杂,能够成功导入的球队很少,在应用上不如挡拆战术广泛。NBA在NBA,最早使用这套战术的是菲尔·杰克逊。在菲尔·杰克逊担任总教练之前,底特律活塞两度在东区决赛中击败芝加哥公牛,他们设计了乔丹法则来专门防守麦可·乔登。菲尔·杰克逊说服麦可·乔登交出球权,分享给队友,在泰斯·温特(英语:TexWinter)的协助下,将三角战术战术导入芝加哥公牛,协助公牛获得六次NBA总冠军。以麦可·乔登、史考提·皮朋两人为球队中心,在前期,两人与霍雷斯·格兰特形成三角,后期,则由丹尼斯·罗德曼搭配。1999年,菲尔·杰克逊任洛杉矶湖人总教练,导入三角战术。前期以侠客·欧尼尔及科比·布莱恩特为中心,配合霍雷斯·格兰特、格伦·莱斯、罗伯特
· 三角翼

历史第一种双发三角翼飞机——F-102战斗机采用鸭式前翼布局的台风战斗机关于三角翼的概念,最早可以依靠历史文献追溯至16世纪。1529年至1556年间,率先提出多节火箭概念的奥地利工程师康拉德·夏斯(ConradHaas)在其一本讲述火箭、烟火、武器技术的著作中,不但提及多节火箭的原理和液体燃料混合技术,更提出了采用三角形平面作为火箭稳定翼的构思。这份手稿于1961年在罗马尼亚锡比乌公共档案中首次被发现(SibiupublicrecordsVariaII374)。至17世纪,波兰立陶宛联邦的军事工程师卡齐米日·西门诺维兹(KazimierzSiemienowicz)也再次提出了类似的方案。如同后掠翼,现代三角翼的发展也源于德国。德国著名空气动力学家亚历山大·李比希(AlexanderLippisch)至1920年代开始就致力于无尾三角翼的研究,并曾经与霍尔滕兄弟(Hortenbrother...
· 火三角

火四面体火四面体随着科学的发展,人们发现用燃烧三角形来表示“无火焰燃烧”是确切的;但对于“有火焰燃烧”,因为燃烧过程中存在未受抑制的分解物(游离基)作为中间体,作为链式反应。所以表示有火焰燃烧应增加一个必要条件──链式反应,这样就形成了燃烧四面体。可燃物在燃烧前会裂解为简单的分子,分子中的共价键在外界因素(如光、热)的影响下,裂解而成化学活性非常强的原子或原子团──称为游离基。有氢原子、氧原子及羟基等。链式反应大多数的有火焰燃烧都存在着链式反应。当某种可燃物受热时,它不仅会气化,而且该可燃物的分子还会发生热裂解作用,即它们在燃烧前会裂解为简单分子,活性很强的游离基。由于游离基是一种高度活泼的化学形态,能与其他的游离基及分子产生反应,而使燃烧持续下去,这就产生了燃烧的链式反应。应用一场火灾通过燃烧过程,其化学反应使之温度更高并能持续下去,传统的“火三角”能应用在不少火灾上,但如果火灾涉及到锂...
· 三角柱
相关多面体与镶嵌三角柱可以由三角形二面体的对偶三面形透过截角变换构造而来,因此与三角形二面体具有相同的对称性,其可以衍生出一些相关的多面体:参见半正多面体
· 三角学

历史第一个三角函数表是由喜帕恰斯编制而成的,他被后世称为“三角学之父”。苏美尔天文学家引入了角度测量,将一个圆分割为360度。他们和之后的巴比伦人都在研究相似三角形各边之间的比例关系,并发现了其中一部分比例,但是并没有将其发展为一套系统的方法。古代努比亚人也使用了类似的方法。古希腊人最早将三角学转变成一套系统学科。穆斯林天文学家巴塔尼引入了我们今天熟知的正弦、余弦、正切、余切等术语,并且提出了正切(称为“阴影”,阿拉伯语:ظل)和余切的概念。明代末年,由于历法改革的需要,西学东渐中陆续引进了几何学、三角学等西方数学。这项工作仍在清朝继续进行,其中最重要的是由波兰传教士穆尼阁和薛凤祚所介绍的对数方法。薛凤祚所著《历学会通》的数学部分主要是传自穆尼阁的《比例对数表》(1653年)、《比例四线新表》和《三角算法》等各一卷。《比例对数表》和《比例四线新表》分别给出了1~10000的六位对数表和六位...
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信















