形式

对于任意实数x{\displaystyle x\,}，以下恒真：

由此也可以推导出 sin⁡ ⁡ -->x=eix− − -->e− − -->ix2i{\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}及cos⁡ ⁡ -->x=eix+e− − -->ix2{\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}}。 当x=π π -->{\displa欧拉tyle x=\pi \,}时，欧拉公式的特殊形式为eiπ π -->+1=0{\displaystyle欧拉恒等式\pi }+1=0\,}。（参见欧拉恒等式）

cis函数

在复分析领域，欧拉公式亦可以以函数的形式表示

并且一般定义域为θ θ -->∈ ∈ -->R{\displaystyle \theta \in \mathbb {R} \,}，值域为θ θ -->∈ ∈ -->C{\displaystyle \theta \in \mathbb {C} \,}（复平面上的所有单位向量）。

当一复数的模为1，其反函数就是辐角（arg函数）。

当θ θ -->{\displaystyle \theta }值为复数时，cis函数仍然是有效的，所以有些人可利用cis函数将欧拉公式推广到更复杂的版本。

证明

对于所有x∈ ∈ -->I{\displaystyle x\in I}，定义函数f(x)=cos⁡ ⁡ -->x+isin⁡ ⁡ -->xeix{\displaystyle f(x)={\frac {\cos x+i\sin x}{e^{ix}}}}

由于eix⋅ ⋅ -->e− − -->ix=e0=1{\displaystyle e^{ix}\cdot e^{-ix}=e^{0}=1}

可知eix{\displaystyle e^{ix}\,}不可能为0，因此以上定义成立。

f(x){\displaystyle f(x)\,}之导数为：

设 [a,b]∈ ∈ -->I{\displaystyle [a,b]\in I} 和 c∈ ∈ -->(a,b){\displaystyle c\in (a,b)}

因此f(x){\displaystyle f(x)\,}必是常数函数。

重新整理，即可得到：

找出一个函数，使得dydx=iy{\displaystyle {\frac {dy}{dx}}=iy}及f(0)=1{\displaystyle f(0)=1}

如果使用积分法，iy{\displaystyle iy}的原函数是以上两个函数。

x=0{\displaystyle x=0} 时，原函数的值相等，所以以上两个函数相等。

证明和角公式

由于eiα α -->=cos⁡ ⁡ -->α α -->+isin⁡ ⁡ -->α α -->{\displaystyle e^{i\alpha }=\cos \alpha +i\sin \alpha }且eiβ β -->=cos⁡ ⁡ -->β β -->+isin⁡ ⁡ -->β β -->{\displaystyle e^{i\beta }=\cos \beta +i\sin \beta }，将两式相乘，则

实部等于实部，虚部等于虚部，因此

在复变分析的应用

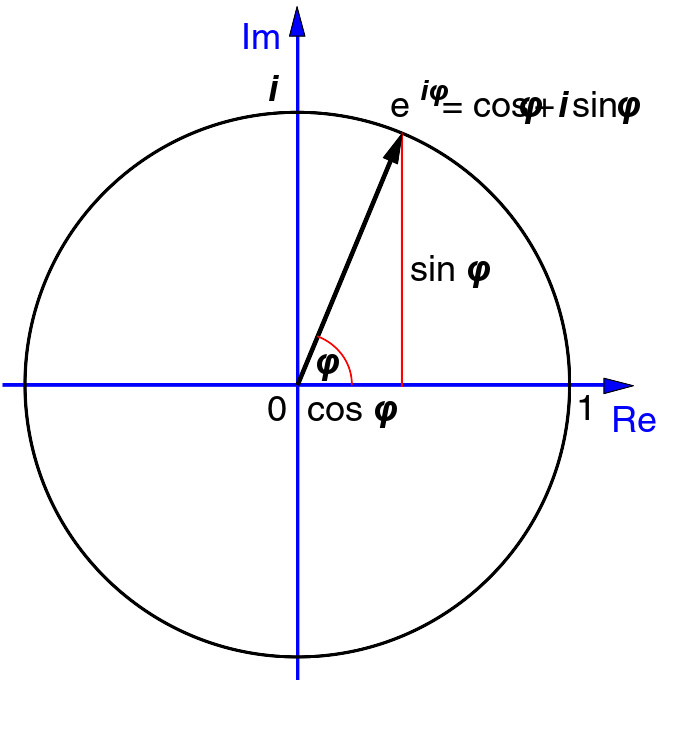
这公式可以说明当x{\displaystyle x}为实数时，函数eix{\displaystyle e^{ix}}可在复数平面描述一单位圆。且x{\displaystyle x}为此平面上一条连至原点的线与正实轴的交角。 先前一个在复平面的复点只能用笛卡尔坐标系描述，欧拉公式在此提供复点至极坐标的变换

任何复数z=x+yi{\displaystyle z=x+yi}皆可记为

在此

参见

cis函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。