基本介绍

圆群上的加法

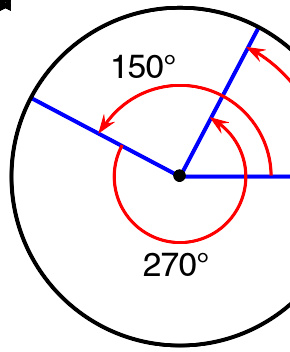
思考圆群的一种方法是描述其“角度”如何相加，其中只有0至360度的角度是被允许的。例如，右边的图表描述著如何将150度加上270度。其答案应该是150度+270度=420度，但以圆群的观点来考虑，而必须要“忘记”扫过一整个圆的事实。因此，必须以360度来调整其答案，如此将会得出420度−360度=60度之答案。

另一种描述方法是使用原本的加法，但数字只限定在0和1之间。要完成此一描述，必须丢掉小数点前的数位。例如，当在算0.784+0.925+0.446时，其答案应该是2.155，但这里必须丢掉前面的2，因此其答案（在圆群中）会是0.155。

拓扑与解析结构

圆群不只是一个抽象代数群而已。当将其视为复平面的子空间时，其会有一个自然的拓扑。因为乘法和反演是在C上的连续函数，圆群会有一拓扑群的结构。更甚地，当单位圆是复平面上的一个闭子集时，圆群也会是C（其自身被视为是一拓扑群）的闭子群。

更多地，因为圆是一个一维实流形且其乘法和反演为圆上的圆变映射，这给了圆群一个一维李群的结构。实际上，以同构来分，其为唯一的一个同构于T的一维紧致连通李群

同构

圆群在数学里可承现出很多种不同的类型。下面列出较常见的几种类型，并证明

由所有一阶酉矩阵（即单位复数）所组成之群显然与圆群相对应；其酉的条件即等价于其元素的模为1的条件。因此圆群会同构于第一个酉群U(1)。

指数函数会产生一个由实数加法群R映射至圆群T上之群同态exp:R→T，其映射为

其最后一个等式为欧拉公式。实数θ会对应到单位圆上由正x轴量起的角度。这个映射是一个同态，因为单位复数的乘法可以对应到角度的加法上：

此一指数映射很明显地是一个由R映射至T的满射函数，但它不是单射。这个映射的核为所有2π整数倍之集合。基于第一同构定理，会有着

调整一下尺度后，也可以说T同构于R/Z。

若将复数视为二阶实矩阵（见复数），单位复数则会对应至有单位行列式的二阶正交矩阵上。具体地说，会有如下之对应关系

圆群因此会同构于特殊正交群SO(2)。此处有着一个单位复数之乘法的几何解释，即为复平面上的旋转，并且任何旋转都可表达成这种形式。

性质

任何大于0之维度的紧致李群G都会有一个会同构于圆群的子群。这是指以对称的观点来思考，一“连续”作用的紧致对称群可以被表示成有一作用着的单参数圆子群；其在物理系统上的结果可以有如旋转不变性和自发性对称破坏等例子。

圆群有许多个子群，但其纯紧致子群只由单位根所构成。

表示

圆群的表示是很容易描述的。舒尔引理描述说一个阿贝尔群的所有不可约复表示都是一维的。圆群是紧致的，任一表示ρ ρ -->: : -->T→ → -->GL1(C)≅ ≅ -->C× × -->{\displaystyle \rho \colon \mathbb {T} \to \mathrm {GL} _{1}(\mathbb {C} )\cong \mathbb {C} ^{\times }}都必须在U(1)≅ ≅ -->T{\displaystyle \mathrm {U} (1)\cong \mathbb {T} }内取值。因此，圆群的不可约表示只是个由圆群映射至其本身的同态。每一个如此的同态都会有下面的形式

这些表示都是等价的。表示ϕ ϕ -->− − -->n{\displaystyle \phi _{-n}} 共轭于ϕ ϕ -->n{\displaystyle \phi _{n}}

这些表示都只是圆群的特征标。而T的特征标群明显为由ϕ ϕ -->1{\displaystyle \phi _{1}}所产生之无限循环群：

圆群的不可约实数表示为（一维的）当然表示，且其表示

的值在SO(2)内。这里只有正整数n，因为表示ρ ρ -->− − -->n{\displaystyle \rho _{-n}}会等价于ρ ρ -->n{\displaystyle \rho _{n}}。

代数结构

在此一章节中将不提及圆群的拓扑结构，而只专注于其代数结构。

圆群T是一个可除群。其挠子群是由所有n次单位根所组成之集合，且会同构于Q/Z。可除群的结构定理表示T会同构于Q/Z和一串Q的直积。这一串Q的数目必须为c（连续势）为了使直积的势会是正确的。但c个Q的直积会同构于R，R如同是在Q上的c维向量空间。因此

同构

也可以以同样的方式证明，因为C也是其挠子群和T的挠子群相同的可除阿贝尔群。

另见

环面

单参数子群

酉群

正交群

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。