理论所有原子的量子态都束聚于一个单一的量子态的状态被称为玻色凝聚或玻色-爱因斯坦凝聚。1920年代，萨特延德拉·纳特·玻色和阿尔伯特·爱因斯坦以玻色关于光子的统计力学研究为基础，对这个状态做了预言。2005年7月22日，乌得勒支大学的学生罗迪·玻因克在保罗·埃伦费斯特的个人档案中发现了1924年12月爱因斯坦手写的原文的草稿。玻色和爱因斯坦的研究的结果是遵守玻色-爱因斯坦统计的玻色气体。玻色-爱因斯坦统计是描写玻色子的统计分布的理论。玻色子，其中包括光子和氦-4之类的原子，可以分享同一量子态。爱因斯坦推测将玻色子冷却到非常低的温度后它们会“落入”（“凝聚”）到能量最低的可能量子态中，导致一种全新的相态。一个单纯的三维的气体的临界温度为（气体处在的外部势能是恒定的）：其中：发现1938年，彼得·卡皮查、约翰·艾伦和冬·麦色纳（DonMisener）发现氦-4在降温到2.2K时会成为一种叫做超...

发展简史玻色子具有整数自旋，并遵守玻色-爱因斯坦统计。萨特延德拉·纳特·玻色阐明了光子的表现，并为统计力学遵从量子规则的微系统提供了机会，1924年写了一篇推导普朗克量子辐射定律的论文寄给当时在德国的爱因斯坦，爱因斯坦意识到这篇论文的重要性，并将其扩展到不同的经典理想气体的宏观粒子（英语：Massiveparticle），不但亲自把它翻译成德语，还以玻色的名义把论文递予名望颇高的《德国物理学刊》（"ZeitschriftfürPhysik"）发表。延伸阅读费米气体全同粒子盒中气体德拜模型玻色子玻色-爱因斯坦统计玻色–爱因斯坦凝聚参考资料Bosegas

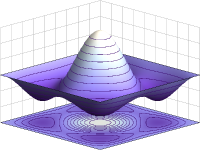
定义与性质在无限深方形阱里，两个全同玻色子的对称波函数绘图。玻色子定义为遵守玻色-爱因斯坦统计的粒子；根据玻色-爱因斯坦统计，对于N个全同玻色子，假设将其中任意两个玻色子交换，则由于描述这量子系统的波函数具有对称性，波函数不会改变。费米子遵守费米狄拉克统计；根据费米狄拉克统计，对于N个全同费米子，假设将其中任意两个费米子交换，则由于描述这量子系统的波函数具有反对称性，波函数的正负号会改变。由于这特性，费米子遵守包利不相容原理：两个全同费米子不能占有同样的量子态。因此，物质具有有限体积与硬度。费米子被称为物质的组成成分。所有已知基本或复合粒子，依照自旋而定，自旋为整数的粒子是玻色子，自旋为半整数的粒子是费米子。在非相对论性量子力学里，这纯为经验观察；但在相对论性量子场论里，自旋统计定理表明，半整数的粒子不能成为玻色子，整数的粒子不能成为费米子。激光、激微波、超流体、玻色-爱因斯坦凝聚的基础物...

外部链接官方网站（希伯来文）英文版官方网站

参考文献参见量子统计盒中气体理想气体全同粒子