形式定义

所谓考克斯特群，是一个群 W{\displaystyle W} 配上如下的展示（即一组生成元与关系）：

其中 mij∈ ∈ -->N∪ ∪ -->{∞ ∞ -->}{\displaystyle m_{ij}\in \mathbb {N} \cup \{\infty \}} 满足

对称性－ mij=mji{\displaystyle m_{ij}=m_{ji}}

i≠ ≠ -->j⇒ ⇒ -->mij≥ ≥ -->2{\displaystyle i\neq j\Rightarrow m_{ij}\geq 2}

mii=1{\displaystyle m_{ii}=1}

在此 mij=∞ ∞ -->{\displaystyle m_{ij}=\infty } 意指 ri,rj{\displaystyle r_{i},r_{j}} 之间没有关系。注意到性质三蕴含 ri2=e{\displaystyle r_{i}^{2}=e}；若mij=2{\displaystyle m_{ij}=2}，则 rirj=rjri{\displaystyle r_{i}r_{j}=r_{j}r_{i}}。

令这组生成元为 S{\displaystyle S}。资料 (W,S){\displaystyle (W,S)} 称为考克斯特群。方阵 (mij)ij{\displaystyle (m_{ij})_{ij}} 称为考克斯特矩阵。

性质

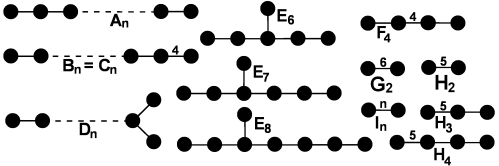
有限考克斯特群的分类

设 (W,S){\displaystyle (W,S)} 为考克斯特群，可证明存在一个有限维实矢量空间 V{\displaystyle V} 及其上的非退化双线性形q{\displaystyle q}（未必正定），使得 W{\displaystyle W} 同构于正交群 O(q){\displaystyle O(q)} 的某个子群。由于 S{\displaystyle S} 的元素均为二阶，可视之为 (V,q){\displaystyle (V,q)} 中对某些超平面的镜射。

利用 (W,S){\displaystyle (W,S)} 的展示，定义元素的长度如下：对 w∈ ∈ -->W{\displaystyle w\in W}，定义其长度 ℓ ℓ -->(w){\displaystyle \ell (w)} 为所有表法 w=ri1⋯ ⋯ -->ris(rj∈ ∈ -->S){\displaystyle w=r_{i_{1}}\cdots r_{i_{s}}\;(r_{j}\in S)} 中最短的 s{\displaystyle s}。由此可导出

例子

对称群 Sn{\displaystyle S_{n}} 是考克斯特群。在此可取 S{\displaystyle S} 为置换 (1,2),(2,3),… … -->,(n− − -->1,n){\displaystyle (1,2),(2,3),\ldots ,(n-1,n)}；关系为 ((k,k+1)(k+1,k+2))3=1{\displaystyle ((k,k+1)(k+1,k+2))^{3}=1}。

正多胞体的对称：正多胞体的对称群是有限考克斯特群。举例明之：正多边形的对称群是二面体群，正 n 维单形的对称群是前述的 Sn+1{\displaystyle S_{n+1}}，又称为 An{\displaystyle A_{n}} 型的考克斯特群。n 维超正方体的对称群为 BCn{\displaystyle BC_{n}}。正十二面体与正二十面体的对称群是 H3{\displaystyle H_{3}}。在四维空间中，存在三种特别的正多胞体──正二十四胞体、正一百二十胞体与正六百胞体，其对称群分别是 F4,H4,H4{\displaystyle F_{4},H_{4},H_{4}}。Dn,E6,E7,E8{\displaystyle D_{n},E_{6},E_{7},E_{8}} 可以由某些半正多胞体的对称群得到。

外尔群：每个根系的外尔群都是有限考克斯特群。

仿射外尔群：仿射外尔群是无限群，但带有一个正则阿贝尔子群，使得对应的商群是个外尔群。

分类

一般而言，两个群展示的同构与否是无法判定的。然而对考克斯特群则有一个简单的判准，称为交换条件。可以透过考克斯特-丹金图分类有限考克斯特群。图的构造方式为：

每个生成元对应到一个顶点。

若 mij≥ ≥ -->3{\displaystyle m_{ij}\geq 3}，则顶点 ri,rj{\displaystyle r_{i},r_{j}} 之间有边相连。

若 mij≥ ≥ -->4{\displaystyle m_{ij}\geq 4}，则将边标上 mij{\displaystyle m_{ij}}。

文献

Larry C Grove and Clark T. Benson, Finite Reflection Groups (1985), Graduate texts in mathematics, vol. 99, Springer.

Paul Garrett, Buildings and Classical Groups (1997), Chapman Hall. ISBN 0-412-06331-X .PostScript 档案下载.

James E. Humphreys, Reflection Groups and Coxeter Groups (1990), Cambridge studies in advanced mathematics, 29.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。