笛卡儿积的性质

易见笛卡儿积满足下列性质：

对于任意集合 A {\displaystyle A} ，根据定义有 A × × --> ∅ ∅ --> = ∅ ∅ --> × × --> A = ∅ ∅ --> {\displaystyle A\times \varnothing =\varnothing \times A=\varnothing }

一般来说笛卡儿积不满换律和结合律。

笛卡儿积对集合的并和交满足分配律，即

笛卡儿平方和n元乘积

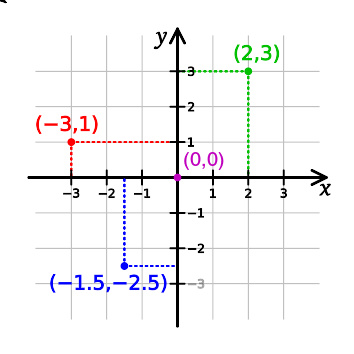
集合 X 的 笛卡儿平方 （或 二元笛卡儿积 ）是笛卡儿积 X × X 。一个例子是二维平面 R × R ，（这里 R 是实数集） - 它包含所有的点( x , y )，这里的 x 和 y 是实数（参见笛卡儿坐标系）。

为了帮助枚举，可绘制一个表格。一个集合作为行而另一个集合作为列，从行和列的集合选择元素，以形成有序对作为表的单元格。

可以推广到在 n 个集合 X 1 , ..., X n 上的 n -元笛卡儿积 :

实际上，它可以被等同为 ( X 1 × ... × X n-1 ) × X n 。它是n -元组的集合。

一个例子是欧几里得三维空间 R × R × R ，这里的 R 同样是指实数集。

无穷乘积

对最常用的数学应用而言，上述定义通常已经足够。但是，也可以在任意（可能无限）的集合的搜集上定义笛卡儿积。如果 I 是任何指标集合，而

是由 I 索引的集合的搜集，则我们定义

就是定义在索引集合上的所有函数的集合，使得这些函数在特定索引 i 上的值是 X i 的元素。

对在 I 中每个 j ，定义自

的函数

叫做 第 j 投影映射 。

n -元组可以被看作在{1, 2, ..., n }上的函数，它在 i 上的值是这个元组的第 i 个元素。所以，在 I 是{1, 2, ..., n }的时候，这个定义跟有限情况的定义是一致的。在无限情况下这个定义给出的是集合族。

在无限情况，一个令人熟悉的特例是，当索引集合是自然数集 N , {\displaystyle \mathbb {N} ,} 的时候：这正是其中第 i 项对应于集合 X i 的所有无限序列的集合。再次， R {\displaystyle \mathbb {R} } 提供了这样的一个例子：

是实数的无限序列的搜集，可视之为带有无限个构件的向量或元组。另一个特殊情况（上述例子也满足它）是在乘积中的各因子 X i 都是相同的时候，类似于“笛卡儿指数”。这样，在最先定义中的无限并集自身就是这个集合自身，而其他条件被平凡的满足了，所以这正是从 I 到 X 的所有函数的集合。

在别的情况，无限笛卡儿积就不那么直观了；尽管在高等数学中的应用有其价值。

“非空集合的任意非空搜集的笛卡儿积为非空”这一陈述等价于选择公理。

函数的笛卡儿积

如果 f 是从 A 到 B 的函数，而 g 是从 X 到 Y 的函数，则它们的 笛卡儿积 f × g 是从 A × X 到 B × Y 的函数，带有

跟之前类似，函数的笛卡儿积也可以扩展到函数的元组和无限情况。

参见

有序对

幂集公理

二元关系

笛卡儿

乘积拓扑

乘积 (范畴论)

拉回 (范畴论)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。