数学定义

令 G = ( I , E )表示一个 有向无环图 （DAG），其中 I 代表图形中所有的节点的集合，而 E 代表有向连接线段的集合，且令 X = ( X i ) i ∈ I 为其有向无环图中的某一节点 i 所代表之随机变量，若节点 X 的联合概率分配可以表示成：

则称X为相对于一有向无环图G的贝叶斯网络，其中 p a ( i ) {\displaystyle pa(i)} 表示节点i之“因”。

对任意的随机变量，其联合分配可由各自的局部条件概率分配相乘而得出：

依照上式，我们可以将一贝叶斯网络的联合概率分配写成：

上面两个表示式之差别在于条件概率的部分，在贝叶斯网络中，若已知其“因”变量下，某些节点会与其“因”变量条件独立，只有与“因”变量有关的节点才会有条件概率的存在。

如果联合分配的相依数目很稀少时，使用贝氏函数的方法可以节省相当大的内存容量。举例而言，若想将10个变量其值皆为0或1存储成一条件概率表型式，一个直观的想法可知我们总共必须要计算 2 10 = 1024 {\displaystyle 2^{10}=1024} 个值；但若这10个变量中无任何变量之相关“因”变量是超过三个以上的话，则贝叶斯网络的条件概率表最多只需计算 10 ∗ ∗ --> 2 3 = 80 {\displaystyle 10*2^{3}=80} 个值即可！另一个贝式网络优点在于：对人类而言，它更能轻易地得知各变量间是否条件独立或相依与其 局部分配 （local distribution）的类型来求得所有随机变量之联合分配。

马尔可夫毯（Markov blanket）

定义一个节点之马尔可夫毯为此节点的因节点、果节点与果节点的因节点所成之集合。一旦给定其马尔可夫毯的值后，若网络内之任一节点 X 皆会与其他的节点条件独立的话，就称 X 为相对于一有向无环图 G 的贝叶斯网络。

举例说明

假设有两个服务器 ( S 1 , S 2 ) {\displaystyle (S_{1},S_{2})} ，会发送数据包到用户端（以 U 表示之），但是第二个服务器的数据包发送成功率会与第一个服务器发送成功与否有关，因此此贝叶斯网络的结构图可以表示成如图二的型式。就每个数据包发送而言，只有两种可能值： T （成功）或 F （失败）。则此贝叶斯网络之联合概率分配可以表示成：

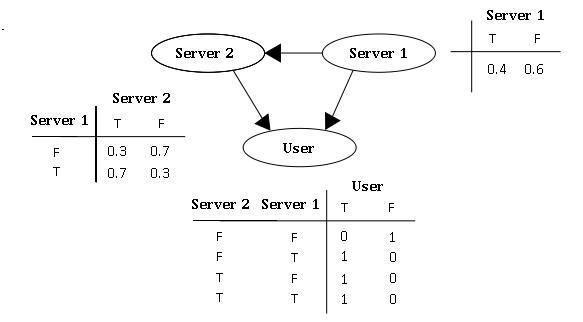
图二：简单的贝叶斯网络例子

此模型亦可回答如：“假设已知用户端成功接受到数据包，求第一服务器成功发送数据包的概率?”诸如此类的问题，而此类型问题皆可用条件概率的方法来算出其所求之发生概率：

求解方法

以上例子是一个很简单的贝叶斯网络模型，但是如果当模型很复杂时，这时使用枚举式的方法来求解概率就会变得非常复杂且难以计算，因此必须使用其他的替代方法。一般来说，贝氏概率有以下几种求法：

精确推理

枚举推理法（如上述例子）

变量消元算法（variable elimination）

随机推理（蒙特卡洛方法）

直接取样算法

拒绝取样算法

概似加权算法

马尔可夫链蒙特卡洛算法（Markov chain Monte Carlo algorithm）

在此，以马尔可夫链蒙特卡洛算法为例，又马尔可夫链蒙特卡洛算法的类型很多，故在这里只说明其中一种Gibbs sampling的操作步骤： 首先将已给定数值的变量固定，然后将未给定数值的其他变量随意给定一个初始值，接着进入以下迭代步骤：

当迭代结丛后，删除前面若干笔尚未稳定的数值，就可以求出的近似条件概率分配。马尔可夫链蒙特卡洛算法的优点是在计算很大的网络时效率很好，但缺点是所抽取出的样本并不具独立性。

当贝叶斯网络上的结构跟参数皆已知时，我们可以通过以上方法来求得特定情况的概率，不过，如果当网络的结构或参数未知时，我们必须借由所观测到的数据去推估网络的结构或参数，一般而言，推估网络的结构会比推估节点上的参数来的困难。依照对贝叶斯网络结构的了解和观测值的完整与否，我们可以分成下列四种情形：

以下就结构已知的部分，作进一步的说明。

1.结构已知，观测值完整：

此时我们可以用最大似然估计法（MLE）来求得参数。其对数概似函数为

其中 p a ( X i ) {\displaystyle pa(X_{i})} 代表 X i {\displaystyle X_{i}} 的因变量， D i {\displaystyle D_{i}} 代表第 1 {\displaystyle {\mathit {1}}} 个观测值， N 代表观测值数据的总数。

以图二当例子，我们可以求出节点 U 的最大似然估计式为

由上式就可以借由观测值来估计出节点 U 的条件分配。如果当模型很复杂时，这时可能就要利用数值分析或其它最优化技巧来求出参数。

2.结构已知，观测值不完整（有遗漏数据）：

如果有些节点观测不到的话，可以使用EM算法（ Expectation-Maximization algorithm ）来决定出参数的区域最佳概似估计式。而EM算法的的主要精神在于如果所有节点的值都已知下，在M阶段就会很简单，如同最大似然估计法。而EM算法的步骤如下：

其中 E N ( x ) {\displaystyle EN(x)} 代表在目前的估计参数下，事件x的条件概率期望值为

补充例子（枚举推理法）

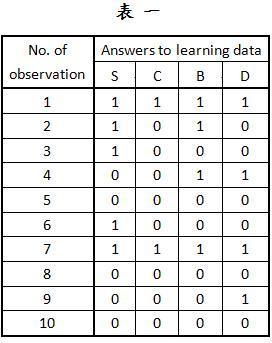
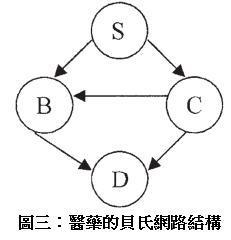
让我们考虑一个应用在医药上的概率推论例子，在此病人会被诊断出是否有呼吸困难的症状。表一代表一个我们所观测到的数据集合，包含10笔观测值， S 代表的是吸烟与否（Smoker）， C 代表是否为罹癌者（Cancer）， B 代表是否罹患支气管炎（bronchitis）， D 代表是否有呼吸困难及咳嗽（dyspnea and asthma）的症状。‘1’和‘0’分别代表‘是’和‘否’。此医药网络结构显示于图三。

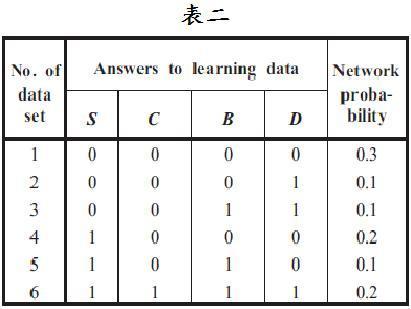
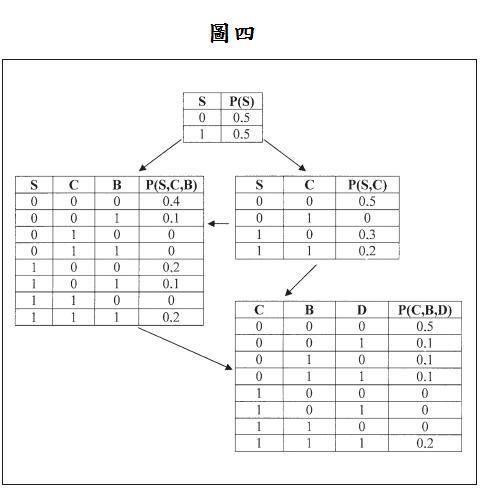
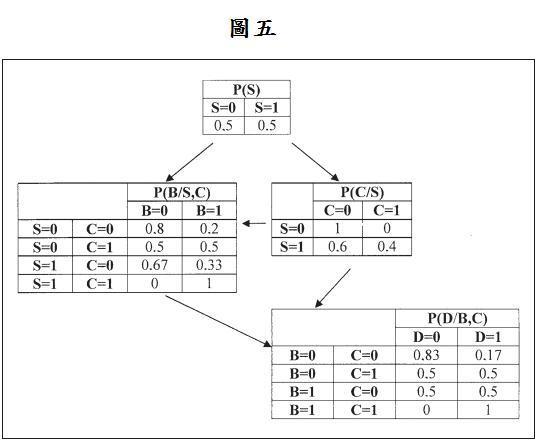
表二代表的是整个网络的经验联合概率分配，是由所收集到的数据所建构而成，利用此表可建构出节点的联合概率分配。见图四。此贝氏公式 P ( A | B ) = P ( A , B ) P ( B ) {\displaystyle P(A|B)={\frac {P(A,B)}{P(B)}}} 可利用节点的边际概率和联合概率去计算节点的条件概率，待会会应用在创建 条件概率表格 （Conditional probability Table; CPT）上。见图五。贝叶斯网络的联合概率可由下列式子计算：

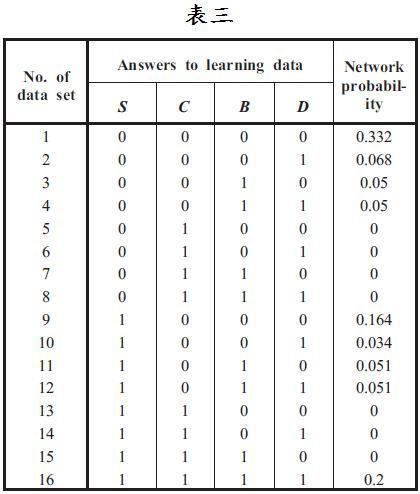
其值见表三。

使用整个网络经验联合概率分配所计算出来的值会与使用CPT所计算出来的值不同，其差异可由表二和表三得知。其中差异不只是值的不同，也出现了新事件的概率（原本所没观察到的事件）。

创建在观测数据上的概率推论算法：

使用表一的观测值和图一的贝叶斯网络结构，并且已知示例点（instantiated node）为 { S = 0 , C = 0 } {\displaystyle \left\{S=0,C=0\right\}} ，也就是病人为非吸烟者和罹癌者： P ( S = 0 ) = 1 , P ( C = 0 ) = 1 {\displaystyle P\left(S=0\right)=1,P\left(C=0\right)=1}

问题： 1.病人患有支气管炎的概率 P ( B ) = ? {\displaystyle P\left(B\right)=?} 2.病人会有呼吸困难的概率 P ( D ) = ? {\displaystyle P\left(D\right)=?}

解答： 1. P ( B = 0 | S = 0 , C = 0 ) = 0.8 {\displaystyle P\left(B=0|S=0,C=0\right)=0.8}

2. P ( D = 0 | S = 0 , C = 0 ) {\displaystyle P\left(D=0|S=0,C=0\right)}

贝叶斯网络的应用层面

贝叶斯网络目前应用在类比计算生物学（computational biology）与生物信息学（bioinformatics）基因调控网络（gene regulatory networks）、蛋白质结构（protein structure）、基因表达分析（gene expression analysis）、医学（medicine）、文件分类（document classification）、信息检索（information retrieval）、决策支持系统（decision support systems）、工程学（engineering）、游戏与法律（gaming and law）、数据结合（data fusion）、图像处理（image processing）等。

参考文献

A. N. Terent" yev and P. I. Bidyuk. METHOD OF PROBABILISTIC INFERENCE FROM LEARNING DATA IN BAYESIAN NETWORKS. Cybernetics and Systems Analysis, 391-396, Vol. 43, No. 3, 2007

Emilia Mendes and Nile Mosley. Bayesian Network Models for Web Effort Prediction: A Comparative Study. IEEE TRANSACTIONS ON SOFTWARE ENGINEERING, 723-737, VOL. 34, NO. 6, NOVEMBER/DECEMBER 2008

Yu. V. Kapitonova, N. M. Mishchenko, O. D. Felizhanko, and N. N. Shchegoleva. USING BAYESIAN NETWORKS FOR MONITORING COMPUTER USERS. Cybernetics and Systems Analysis, 789-799, Vol. 40, No. 6, 2004

Ben-Gal I., Bayesian Networks, in Ruggeri F., Faltin F. & Kenett R. ,Encyclopedia of Statistics in Quality & Reliability, Wiley & Sons (2007).

Radu Stefan Niculescu, Tom M. Mitchell and R. Bharat Rao, Journal of Machine Learning Research 7 (2006) 1357–1383

N. Terent" yev and P. I. Bidyuk. METHOD OF PROBABILISTIC INFERENCE FROM LEARNING DATA IN BAYESIAN NETWORKS. Cybernetics and Systems Analysis, 391-396, Vol. 43, No. 3, 2007

P. I. Bidyuk, A. N. Terent’ev, and A. S. Gasanov. CONSTRUCTION AND METHODS OF LEARNING OF BAYESIAN NETWORKS. Cybernetics and Systems Analysis, 587-598, Vol. 41, No. 4, 2005

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。