直观诠释：二维环面的情形

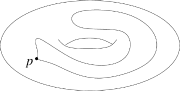
二维环面上由p点出发的环路

首先，让我们考虑二维环面（或者可以想象成甜甜圈的表面）的例子作为热身，固定其上一点p{\displaystyle p}。

从此点出发，则可以建构环路（即：从p{\displaystyle p}出发的并回到p{\displaystyle p}的闭曲线）。设想环路如橡皮筋可自由变形与拉长，只要起点与终点仍是p{\displaystyle p} 且环路仍处在环面上即可。这种变形叫做同伦，若一环路可以从另一环路借此变形而得到，则称两者同伦等价。我们只探讨环路的同伦类。二维环面的基本群由环路的同伦类组成。

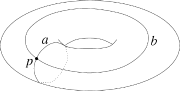
a与b非同伦等价

在上图中，a{\displaystyle a}与b{\displaystyle b}并非同伦等价：无法连续地从一者变换到另一者而不将环路“扯断”，它们代表基本群中的不同元素。借着增加环绕圈数，可以获得更多的同伦类。

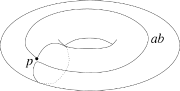
a、b两条环路的衔接

顾名思义，基本群不只是一个集合，它带还有群结构：二元运算由环路的衔接给出，即先走完第一条环路，再走第二条环路，使得两段环路上的速率相同。基本群中的单位元素eP{\displaystyle e_{P}}由静止在p{\displaystyle p}点的环路代表，逆元由环路的逆行代表之，即：若一元素由环路s:[0,1]→ → -->T2{\displaystyle s:[0,1]\to \mathbb {T} ^{2}}代表，则其逆元由s∘ ∘ -->τ τ -->:[0,1]→ → -->T2{\displaystyle s\circ \tau :[0,1]\to \mathbb {T} ^{2}}代表，其中τ τ -->(t)=1− − -->t(t∈ ∈ -->[0,1]){\displaystyle \tau (t)=1-t\quad (t\in [0,1])}。

形式定义

设X{\displaystyle X}为拓扑空间，p{\displaystyle p}为其中定点。一条连续道路是一个连续映射γ γ -->:[0,1]→ → -->X{\displaystyle \gamma :[0,1]\to X}，而一个以p{\displaystyle p}为基点的环路是一条满足γ γ -->(0)=γ γ -->(1)=p{\displaystyle \gamma (0)=\gamma (1)=p}的连续道路。以下若不另外说明，则环路皆以p{\displaystyle p}为基点。

对两条环路γ γ -->0,γ γ -->1{\displaystyle \gamma _{0},\gamma _{1}}，连续函数一个连续函数（保持基点的同伦）H:[0,1]2→ → -->X{\displaystyle H:\;[0,1]^{2}\to X}使得

∀ ∀ -->t∈ ∈ -->[0,1],H(t,0)=γ γ -->0(t){\displaystyle \forall t\in [0,1],\,H(t,0)=\gamma _{0}(t)}

∀ ∀ -->t∈ ∈ -->[0,1],H(t,1)=γ γ -->1(t){\displaystyle \forall t\in [0,1],\,H(t,1)=\gamma _{1}(t)}

∀ ∀ -->x∈ ∈ -->[0,1],H(0,x)=H(1,x)=p{\displaystyle \forall x\in [0,1],\,H(0,x)=H(1,x)=p}

则称两者同伦等价。不难验证此关系确为等价关系。因此我们可考虑环路对此关系的等价类，以[γ γ -->]{\displaystyle [\gamma ]}表一环路γ γ -->{\displaystyle \gamma }隶属的等价类，亦称同伦类。

现在定两条环路f,g{\displaystyle f,g}的衔接为： (f∗ ∗ -->g)(t)={f(2t),t∈ ∈ -->[0,1/2]g(2t− − -->1),t∈ ∈ -->[1/2,1]{\displaystyle (f*g)(t)=\left\{{\begin{matrix}f(2t),&\quad t\in [0,1/2]\\g(2t-1),&\quad t\in [1/2,1]\end{matrix}}\right.}

直观地说，此环路是先走f{\displaystyle f}再走g{\displaystyle g}，每一段都将速度加倍，以在单位时间内走完全程。可证明[f∗ ∗ -->g]{\displaystyle [f*g]}决定于[f],[g]{\displaystyle [f],[g]}，因此可在环路的同伦类上定义二元运算“*”。不难看出此运算满足结合律。

令单位元eP{\displaystyle e_{P}}为环路eP(t)=p{\displaystyle e_{P}(t)=p}（即静止于p{\displaystyle p}点的环路），并令环路f:[0,1]→ → -->X{\displaystyle f:[0,1]\to X}之逆为f− − -->1(t)=f(1− − -->t){\displaystyle f^{-1}(t)=f(1-t)}（即f{\displaystyle f}逆行）。可证明[f]↦ ↦ -->[f− − -->1]{\displaystyle [f]\mapsto [f^{-1}]}在同伦类上有明确定义，且同伦类在此运算下成为一个群。

此群称为X{\displaystyle X}在基点p{\displaystyle p}的基本群，表为π π -->1(X,p){\displaystyle \pi _{1}(X,p)}。

例子

Rn{\displaystyle \mathbb {R} ^{n}}对任何基点的基本群皆为平凡群。换言之，每个环路都可以连续地变形到基点。这类空间称为单连通空间。

当n≥ ≥ -->2{\displaystyle n\geq 2}时，Sn{\displaystyle \mathbb {S} ^{n}}为单连通。

圆环S1{\displaystyle \mathbb {S} ^{1}}之基本群为Z{\displaystyle \mathbb {Z} }。其元素一一对应于em:t↦ ↦ -->e2iπ π -->mt{\displaystyle e_{m}:t\mapsto e^{2i\pi mt}}，其中m∈ ∈ -->Z{\displaystyle m\in \mathbb {Z} }表示环路绕行圆环的次数（计入方向）；群运算由[em]⋅ ⋅ -->[en]=[em+n]{\displaystyle [e_{m}]\cdot [e_{n}]=[e_{m+n}]}给出。一般而言，n{\displaystyle n}维环面的基本群同构于Zn{\displaystyle \mathbb {Z} ^{n}}。

基本群也可能含挠元：例如射影平面RP2{\displaystyle \mathbb {R} P^{2}}的基本群便同构于Z/2Z{\displaystyle \mathbb {Z} /2\mathbb {Z} }。

基本群不一定可交换：例如挖去两点的平面R2− − -->{a,b}{\displaystyle \mathbb {R} ^{2}-\{a,b\}}的基本群同构于两个生成元的自由群，生成元分别对应于绕行a{\displaystyle a}与b{\displaystyle b}的环路。

事实上，可以证明对任何群G{\displaystyle G}皆存在一个拓扑空间，使其基本群同构于G{\displaystyle G}（此空间可以用二维CW复形构造，当群为有限展示时则能以四维流形构造）。

基本性质

对基点的独立性

以下设X{\displaystyle X}为道路连通空间。p,q∈ ∈ -->X{\displaystyle p,q\in X}，则π π -->1(X,p){\displaystyle \pi _{1}(X,p)}同构于π π -->1(X,q){\displaystyle \pi _{1}(X,q)}。这是因为存在一条从p{\displaystyle p}到q{\displaystyle q}的道路γ γ -->{\displaystyle \gamma }，依之定义映射

此映射给出从π π -->1(X,q){\displaystyle \pi _{1}(X,q)}至π π -->1(X,p){\displaystyle \pi _{1}(X,p)}的同构，其逆则为

由此可谈论空间本身的基本群（顶多差一个同构），记为π π -->1(X){\displaystyle \pi _{1}(X)}。基本广群理论也"可以简练地解释基本群对基点的独立性。

对连续映射的函子性

设f{\displaystyle f}为空间(X,p)→ → -->(Y,q){\displaystyle (X,p)\to (Y,q)}的同伦等价，则π π -->1(f){\displaystyle \pi _{1}(f)}为同构。

推论.同胚的空间有相同的基本群。

积空间的基本群

π π -->1(X× × -->Y,(p,q))=π π -->1(X,p)× × -->π π -->1(Y,q){\displaystyle \pi _{1}(X\times Y,(p,q))=\pi _{1}(X,p)\times \pi _{1}(Y,q)}

与第一个同调群的关系

道路连通空间的第一个同调群是基本群的交换化。这是Hurwitz定理的特例。

计算方法与应用

范坎彭（van Kampen）定理

基本群一般不易计算，因为须证明某些环路非同伦等价。当空间可分割为较单纯的空间，而其基本群已知时，范坎彭定理（或塞弗特－范坎彭（Seifert-van Kampen）定理）可以将基本群表为一个归纳极限。

锥定理与射影空间的基本群

对一个拓扑空间X{\displaystyle X}，定义其“锥”CX:=(I× × -->X)/(0× × -->X){\displaystyle CX:=(I\times X)/(0\times X)}，其中I{\displaystyle I}表闭区间[0,1]{\displaystyle [0,1]}。当X=S1{\displaystyle X=\mathbb {S} ^{1}}时，CX{\displaystyle CX}同胚于圆锥。

道路连通空间的锥是单连通的，我们也有自然包含映射X≃ ≃ -->1× × -->X⊂ ⊂ -->CX{\displaystyle X\simeq 1\times X\subset CX}。

设f:X→ → -->Y{\displaystyle f:X\to Y}为连续映射，定义映射锥为

例子：设f{\displaystyle f}为S1{\displaystyle \mathbb {S} ^{1}}到自身的映射z↦ ↦ -->z2{\displaystyle z\mapsto z^{2}}，此时C(f)=RP2{\displaystyle C(f)=\mathbb {R} P^{2}}。

锥定理断言C(f){\displaystyle C(f)}的基本群同构于π π -->1(Y){\displaystyle \pi _{1}(Y)}对f∗ ∗ -->(π π -->1(Y)){\displaystyle f_{*}(\pi _{1}(Y))}的正规化的商

应用：实射影空间之基本群同构于Z/2Z{\displaystyle \mathbb {Z} /2\mathbb {Z} }。

图、曲面与多面体的基本群

图的基本群总是自由群。这点可借着将图沿其最小生成树缩为一束S1{\displaystyle \mathbb {S} ^{1}}看出。

多面体的基本群可以展示为生成元与关系，使得每个关系由多面体的一个面给出。

可定向紧曲面的基本群带一个有2g{\displaystyle 2g}个生成元a1,b1,… … -->,ag,bg{\displaystyle a_{1},b_{1},\ldots ,a_{g},b_{g}}及一个关系a1b1a1− − -->1b1− − -->1a2b2a2− − -->1b2− − -->1… … -->agbgag− − -->1bg− − -->1=1{\displaystyle a_{1}b_{1}a_{1}^{-1}b_{1}^{-1}a_{2}b_{2}a_{2}^{-1}b_{2}^{-1}\ldots a_{g}b_{g}a_{g}^{-1}b_{g}^{-1}=1}的展示。整数g{\displaystyle g}决定于曲面的拓扑结构，称为其亏格。

基本群与覆叠空间

基本群的子群的共轭类一一对应于空间的覆叠的同构类，在此对应下，正规子群对应于伽罗瓦覆叠。

在覆叠空间理论中，业已证明了如果空间有单连通的覆叠空间（例如对局部单连通空间），则基本群同构于万有覆叠空间的自同构群。

推广

基本广群

如果一个小范畴（即：对象与全体态射构成一集合）的所有态射皆可逆，则称之为一个广群。所有广群与其间的函子构成一个范畴。群是只有一个对象的广群。

设G{\displaystyle G}为一广群，对其对象定义下述等价关系：

得到的商集记作π π -->0(G){\displaystyle \pi _{0}(G)}（或曰连通分支），这是从广群范畴到集合范畴的函子。

对每个拓扑空间，以下述方式函子地构造一广群π π -->X{\displaystyle \pi X}：

设X{\displaystyle X}为拓扑空间，令π π -->X{\displaystyle \pi X}的对象为X{\displaystyle X}的点，从点x{\displaystyle x}至y{\displaystyle y}的态射是从x{\displaystyle x}到y{\displaystyle y}的道路的同伦类。同伦等价关系相容于道路的头尾相接，故定义了一个广群π π -->X{\displaystyle \pi X}，称为X{\displaystyle X}的基本广群。

Van Kampen定理在广群的框架下有简练的表述。

设G{\displaystyle G}为广群，而x{\displaystyle x}为其对象（也称作G{\displaystyle G}的点）。Hom(x,x){\displaystyle \mathrm {Hom} (x,x)}在态射合成下成为一个群，记之为π π -->1(G,x){\displaystyle \pi _{1}(G,x)}。注：由于基点选取问题，π π -->1{\displaystyle \pi _{1}}并不能定义一个从广群范畴到群范畴的函子。

一个拓扑空间的基本群可以用基本广群定义为π π -->1(X,x0):=π π -->1(π π -->X,x0){\displaystyle \pi _{1}(X,x_{0}):=\pi _{1}(\pi X,x_{0})}。

高阶同伦群

基本群实则是第一个同伦群，这是符号π π -->1(X,x0){\displaystyle \pi _{1}(X,x_{0})}中“1”的由来。

代数几何中的基本群

基本群亦可抽象地定义为纤维函子的自同构群，此纤维函子对每个带基点的覆叠映射r:(Y,q)→ → -->(X,p){\displaystyle r:(Y,q)\to (X,p)}给出纤维r− − -->1(p){\displaystyle r^{-1}(p)}。

此定义可以推广到代数几何，而之前给出的环路定义则不可。在此我们将拓扑空间的覆叠映射代为平展态射，拓扑空间的基点代为概形上的一个几何点x{\displaystyle x}，而纤维函子F{\displaystyle F}对一平展覆叠f:Y→ → -->X{\displaystyle f:Y\to X}给出几何纤维HomX(x,Y){\displaystyle \mathrm {Hom} _{X}(x,Y)}。此推广源出格罗滕迪克与夏瓦雷。

这套理论可以解释函数域的伽罗瓦理论与黎曼曲面的覆叠理论之联系。

文献

Allen Hatcher, Algebraic Topology (2001), Cambridge University Press. ISBN 0521795400

J. P. May, A Concise Course in Algebraic Topology (1999), Chicago University Press. ISBN 0226511839

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。