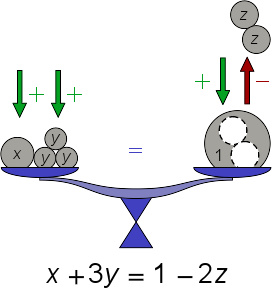
常微分方程

“方程”一词的来历方程一词出现在中国早期的数学专著《九章算术》中，其“卷第八”即名“方程”。卷第八（一）为：翻成白话即为：现在这里有上等黍3捆、中等黍2捆、下等黍1捆，打出的黍共有39斗；有上等黍2捆、中等黍3捆、下等黍1捆，打出的黍共有34斗；有上等黍1捆、中等黍2捆、下等黍3捆，打出的黍共有26斗。问1捆上等黍、1捆中等黍、1捆下等黍各能打出多少斗黍？其“方程术”用阿拉伯数字表示即为：123232311263439{\displaystyle{\begin{array}{*{20}c}1&2&3\\2&3&2\\3&1&1\\{26}&{34}&{39}\\\end{array}}}《九章算术》采用直除法即以一行首项系数乘另一行再对减消元来解方程。若设可打出黍的斗数分别为1捆上等黍x{\displaystylex\,}斗、1捆中等黍y{\displaystyley\,}斗、1捆下等黍z...

公式齐奥尔科夫斯基火箭方程的核心内容是：基于动量守恒原理，任何一个装置，通过一个消耗自身质量的反方向推进系统，可以在原有运行速度上，产生并获得加速度。其认为，任何一次飞行器轨道变化（速度变化）或者多次轨道变化都遵循如下公式:ΔΔ-->v=veln⁡⁡-->m0m1{\displaystyle\Deltav\=v_{e}\ln{\frac{m_{0}}{m_{1}}}}其还可以写成如下方式：m1=m0e−−-->ΔΔ-->v/ve{\displaystylem_{1}=m_{0}e^{-\Deltav\/v_{e}}}或者m0=m1eΔΔ-->v/ve{\displaystylem_{0}=m_{1}e^{\Deltav\/v_{e}}}或者1−−-->m1m0=1−−-->e−−-->ΔΔ-->v/ve{\displaystyle1-{\frac{m_{1}}{m_{0}}}=1-e^{-...

简介考虑一个具一般性的例子，有一个以下的方程：其中x1,...,xn为未知数，而c为常数。其解为反像集合的成员其中T1×···×Tn为函数ƒ的定义域。注意解集合可能为空集合（没有解）、单元素集合（唯一解）、有限个元素的集合及无限多个元素的集合（有无限多的解）。例如，以下的方程：其未知数为x,y及z，可以在等式二侧同减21z，得到以下的式子：以此例而言，方程不会只有唯一解，方程解的个数有无限多个，可以写为以下的集合其中一个特殊解为x=0,y=0,z=0，而x=3,y=6,z=1和x=8,y=9,z=2也是其解。解集合描述一个三维空间中，恰好穿过上述三个点的平面。解集合若解集合（英语：solutionset）为空集合，表示不存在xi使得以下方程成立其中c为一特定常数。例如考虑一个经典的单变数例子，考虑定义域为整数的平方函数ƒ：考...

方程的叙述泊松方程为在这里ΔΔ-->{\displaystyle\Delta}代表的是拉普拉斯算子，而f{\displaystylef}和φφ-->{\displaystyle\varphi}可以实数流形上的实数或复数值的方程。当流形属于欧几里得空间，而拉普拉斯算子通常表示为∇∇-->2{\displaystyle{\nabla}^{2}}，因此泊松方程通常写成在三维直角坐标系，可以写成如果有f(x,y,z){\displaystylef(x,y,z)}恒等于0，这个方程就会变成一个齐次方程，这个方程称作“拉普拉斯方程”。泊松方程可以用格林函数来求解；如何利用格林函数来解泊松方程可以参考screenedPoissonequation。现在有很多种数值解。像是松弛法（英语：relaxationmethod），不断回圈的代数法，就是一个例子。数学表达通常泊松方程表示为这里ΔΔ...

参见渲染