刚体取向

通常，整个刚体的空间位形可以简易地以以下参数设定：

刚体的“位置”：挑选刚体内部一点G来代表整个刚体，通常会设定物体的质心或形心为这一点。从空间参考系S观测，点G的位置就是整个刚体在空间的位置。表示位置可以应用向量的概念。向量的起点为参考系S的原点，终点为点G。设定刚体的位置需要三个坐标，例如，采用直角坐标系，这三个坐标为x-坐标、y-坐标、z-坐标。这用掉了三个自由度。

刚体的取向：描述刚体取向的方法有好几种，包括方向余弦、欧拉角、四元数等等。这些方法设定一个附体参考系B的取向（相对于空间参考系S）。附体参考系是固定于刚体的参考系。相对于刚体，附体参考系的取向固定不变。由于刚体可能会呈加速度运动，所以附体参考系可能不是惯性参考系。空间参考系是某设定惯性参考系，例如，在观测飞机的飞行运动时，附着于飞机场控制塔的参考系可以设定为空间参考系，而附着于飞机的参考系则可设定为附体参考系。刚体的取向需要用到另外三个自由度。

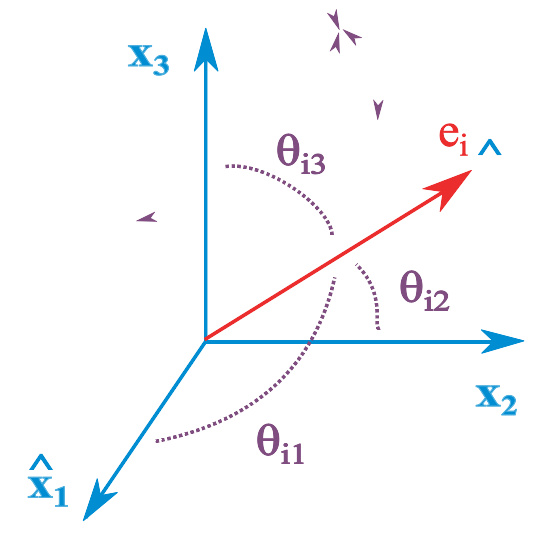
单位向量 ei^ ^ -->{\displaystyle {\hat {\mathbf {e} _{i}}}} 与参考系的三个单位向量 x^ ^ -->1{\displaystyle {\hat {\mathbf {x} }}_{1}} 、x^ ^ -->2{\displaystyle {\hat {\mathbf {x} }}_{2}} 、x^ ^ -->3{\displaystyle {\hat {\mathbf {x} }}_{3}} 之间的夹角分别为 θ θ -->i1{\displaystyle \theta _{i1}} 、θ θ -->i2{\displaystyle \theta _{i2}} 、θ θ -->i3{\displaystyle \theta _{i3}} 。

方向余弦方法可以用来设定附体参考系B的取向，即刚体的取向。假设沿着参考系S的坐标轴的三个单位向量分别为 x^ ^ -->1{\displaystyle {\hat {\mathbf {x} }}_{1}} 、x^ ^ -->2{\displaystyle {\hat {\mathbf {x} }}_{2}} 、x^ ^ -->3{\displaystyle {\hat {\mathbf {x} }}_{3}} ，沿着参考系B的坐标轴的三个单位向量分别为 e^ ^ -->1{\displaystyle {\hat {\mathbf {e} }}_{1}} 、e^ ^ -->2{\displaystyle {\hat {\mathbf {e} }}_{2}} 、e^ ^ -->3{\displaystyle {\hat {\mathbf {e} }}_{3}} 。定义 e^ ^ -->i{\displaystyle {\hat {\mathbf {e} }}_{i}} 与x^ ^ -->j{\displaystyle {\hat {\mathbf {x} }}_{j}} 之间的方向余弦 aij{\displaystyle a_{ij}} 为

其中，θ θ -->ij{\displaystyle \theta _{ij}} 是 e^ ^ -->i{\displaystyle {\hat {\mathbf {e} }}_{i}} 与 x^ ^ -->j{\displaystyle {\hat {\mathbf {x} }}_{j}} 之间的夹角。

e^ ^ -->1{\displaystyle {\hat {\mathbf {e} }}_{1}} 、e^ ^ -->2{\displaystyle {\hat {\mathbf {e} }}_{2}} 、e^ ^ -->3{\displaystyle {\hat {\mathbf {e} }}_{3}} 与 x^ ^ -->1{\displaystyle {\hat {\mathbf {x} }}_{1}} 、x^ ^ -->2{\displaystyle {\hat {\mathbf {x} }}_{2}} 、x^ ^ -->3{\displaystyle {\hat {\mathbf {x} }}_{3}} 之间的关系分别为

两个参考系的坐标轴所形成的矩阵称为“方向余弦矩阵” A{\displaystyle A} ：

采用爱因斯坦求和约定，由于 e^ ^ -->i=aijx^ ^ -->j{\displaystyle {\hat {\mathbf {e} }}_{i}=a_{ij}{\hat {\mathbf {x} }}_{j}} ，给定方向余弦矩阵 A{\displaystyle A} ，则可设定附体参考系B的取向，也就是刚体的取向。

反过来，经过一番运算，可以得到 x^ ^ -->j=aije^ ^ -->i{\displaystyle {\hat {\mathbf {x} }}_{j}=a_{ij}{\hat {\mathbf {e} }}_{i}} 。

给定位置向量 r{\displaystyle \mathbf {r} }

则 r{\displaystyle \mathbf {r} } 与 e^ ^ -->i{\displaystyle {\hat {\mathbf {e} }}_{i}} 的内积为

方向余弦矩阵 A{\displaystyle A} 可以将从空间参考系S观测的位置坐标 (x1,x2,x3){\displaystyle (x_{1},x_{2},x_{3})} ，变换为从附体参考系B观测的位置坐标 (e1,e2,e3){\displaystyle (e_{1},e_{2},e_{3})} ，因此又称为“变换矩阵”。

变换矩阵 A{\displaystyle A} 也可以做反变换如下：

变换矩阵 A{\displaystyle A} 是一种正交矩阵，满足“正交条件”

其中，δ δ -->jk{\displaystyle \delta _{jk}} 是克罗内克函数。

注意到 θ θ -->ij{\displaystyle \theta _{ij}} 与 θ θ -->ji{\displaystyle \theta _{ji}} 不同，夹角 θ θ -->ji{\displaystyle \theta _{ji}} 是e^ ^ -->j{\displaystyle {\hat {\mathbf {e} }}_{j}} 与空间参考系S的坐标轴单位向量 x^ ^ -->i{\displaystyle {\hat {\mathbf {x} }}_{i}} 之间的夹角。变换矩阵 A{\displaystyle A} 通常不是对称矩阵。

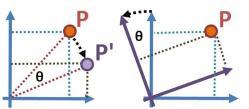
左图显示“主动变换”：参考轴固定不动，点P被旋转 − − -->θ θ -->{\displaystyle -\theta } 角弧成为点P"。右图显示“被动变换”：参考轴被旋转 θ θ -->{\displaystyle \theta } 角弧，而点P固定不动。

变换矩阵 A{\displaystyle A} 可以视为旋转矩阵。例如，将附体参考系B或刚体旋转，从 e^ ^ -->1{\displaystyle {\hat {\mathbf {e} }}_{1}} 、e^ ^ -->2{\displaystyle {\hat {\mathbf {e} }}_{2}} 、e^ ^ -->3{\displaystyle {\hat {\mathbf {e} }}_{3}} 旋转 θ θ -->{\displaystyle \theta } 角弧成为 e^ ^ -->1′{\displaystyle {\hat {\mathbf {e} }}"_{1}} 、e^ ^ -->2′{\displaystyle {\hat {\mathbf {e} }}"_{2}} 、e^ ^ -->3′{\displaystyle {\hat {\mathbf {e} }}"_{3}} ；其中，e^ ^ -->3=e^ ^ -->3′{\displaystyle {\hat {\mathbf {e} }}_{3}={\hat {\mathbf {e} }}"_{3}} 。对于这旋转，旋转矩阵 A{\displaystyle A} 为

参考轴 e^ ^ -->i′{\displaystyle {\hat {\mathbf {e} }}"_{i}} 与 e^ ^ -->j{\displaystyle {\hat {\mathbf {e} }}_{j}} 之间的关系为

旋转矩阵 A{\displaystyle A} 也可以视为将点P的位置向量 r=xix^ ^ -->i{\displaystyle \mathbf {r} =x_{i}{\hat {\mathbf {x} }}_{i}} 旋转 − − -->θ θ -->{\displaystyle -\theta } 角弧成为点P"的位置向量 r′=xi′x^ ^ -->i{\displaystyle \mathbf {r} "=x"_{i}{\hat {\mathbf {x} }}_{i}} ：

参考文献

Tang, K. T. Mathematical Methods for Engineers and Scientists 2. Springer. 2006: 13. ISBN 3540302689. 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。