模型

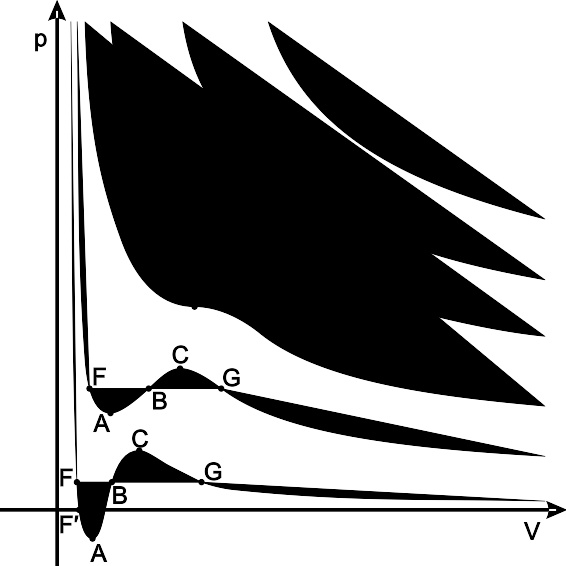
  实际气体的等温线 深蓝线 – 临界温度以下的等温线 绿色区域 – 亚稳态 F点左侧区域 – 普通液体 点F –沸点 线段FG – 液气平衡 FA区域 –过热液体 CG区域– 过冷气体 点G –露点 G点右侧区域 – 普通气体 红线 – 临界等温线 点K –临界点 浅蓝线 – 超临界等温线

范德华（van der Waals）模型

R T = ( P + a V m 2 ) ( V m − − --> b ) {\displaystyle RT=(P+{\frac {a}{V_{m}^{2}}})(V_{m}-b)}

对于上式，a是同分子引力有关的常数，b是同分子自身体积有关的常数，统称为范德华常数，Vm为气体的摩尔体积，p是气体的压强，V是气体的体积，T为热力学温度，R=8.314J·mol·K

雷德利希-邝氏（Redlich–Kwong）模型

雷德利希-邝氏方程是另一个实际气体二元方程。比范德华方程更精确，同时比大多数多元实际气体方程精确。

R T = P ( V m − − --> b ) + a V m ( V m + b ) T 1 2 ( V m − − --> b ) {\displaystyle RT=P(V_{m}-b)+{\frac {a}{V_{m}(V_{m}+b)T^{\frac {1}{2}}}}(V_{m}-b)}

  a {\displaystyle \ a} 为常数，用于修正分子间引力；

  b {\displaystyle \ b} 为常数，用于修正体积。

注意这里的常数a，b与范德华方程中的不同。 a = 0.4275 R 2 T c 2.5 P c {\displaystyle a=0.4275{\frac {R^{2}T_{c}^{2.5}}{P_{c}}}}

b = 0.0867 R T c P c {\displaystyle b=0.0867{\frac {RT_{c}}{P_{c}}}}

贝特罗（Berthelot）模型

贝特罗方程极少使用。

P = R T V m − − --> b − − --> a T V m 2 {\displaystyle P={\frac {RT}{V_{m}-b}}-{\frac {a}{TV_{m}^{2}}}}

修正式更为精确：

P = R T V m [ 1 + 9 P / P c 128 T / T c ( 1 − − --> 6 ( T / T c ) 2 ) ] {\displaystyle P={\frac {RT}{V_{m}}}\left[1+{\frac {9P/P_{c}}{128T/T_{c}}}\left(1-{\frac {6}{(T/T_{c})^{2}}}\right)\right]}

狄特里奇（Dieterici）模型

狄特里奇方程近年来亦很少使用。 P = R T exp ⁡ ⁡ --> ( − − --> a V m R T ) V m − − --> b {\displaystyle P=RT{\frac {\exp {({\frac {-a}{V_{m}RT}})}}{V_{m}-b}}} .

克劳修斯模型（Clausius）

克劳修斯方程是非常简洁的三元实际气体方程。

R T = ( P + a T ( V m + c ) 2 ) ( V m − − --> b ) {\displaystyle RT=\left(P+{\frac {a}{T(V_{m}+c)^{2}}}\right)(V_{m}-b)}

其中

a = 27 R 2 T c 3 64 P c {\displaystyle a={\frac {27R^{2}T_{c}^{3}}{64P_{c}}}}

b = V c − − --> R T c 4 P c {\displaystyle b=V_{c}-{\frac {RT_{c}}{4P_{c}}}}

c = 3 R T c 8 P c − − --> V c {\displaystyle c={\frac {3RT_{c}}{8P_{c}}}-V_{c}}

维里（Virial） 模型

维里方程 P V m = R T ( 1 + B ( T ) V m + C ( T ) V m 2 + D ( T ) V m 3 + . . . ) {\displaystyle PV_{m}=RT\left(1+{\frac {B(T)}{V_{m}}}+{\frac {C(T)}{V_{m}^{2}}}+{\frac {D(T)}{V_{m}^{3}}}+...\right)}

或

P V m = R T ( 1 + B ′ ′ --> ( T ) P + C ′ ′ --> ( T ) P 2 + D ′ ′ --> ( T ) P 3 + . . . ) {\displaystyle PV_{m}=RT\left(1+{\frac {B^{\prime }(T)}{P}}+{\frac {C^{\prime }(T)}{P^{2}}}+{\frac {D^{\prime }(T)}{P^{3}}}+...\right)}

其中 A, B, C, A′, B′, C′ 是温度依赖常数。

彭-罗宾逊（Peng–Robinson） 模型

P = R T V m − − --> b − − --> a ( T ) V m ( V m + b ) + b ( V m − − --> b ) {\displaystyle P={\frac {RT}{V_{m}-b}}-{\frac {a(T)}{V_{m}(V_{m}+b)+b(V_{m}-b)}}}

Wohl 模型

R T = ( P + a T V m ( V m − − --> b ) − − --> c T 2 V m 3 ) ( V m − − --> b ) {\displaystyle RT=\left(P+{\frac {a}{TV_{m}(V_{m}-b)}}-{\frac {c}{T^{2}V_{m}^{3}}}\right)(V_{m}-b)}

其中

a = 6 P c T c V c 2 {\displaystyle a=6P_{c}T_{c}V_{c}^{2}}

b = V c 4 {\displaystyle b={\frac {V_{c}}{4}}}

c = 4 P c T c 2 V c 3 {\displaystyle c=4P_{c}T_{c}^{2}V_{c}^{3}} .

Beattie–Bridgman 模型

P = R T v 2 ( 1 − − --> c v T 3 ) ( v + B ) − − --> A v 2 {\displaystyle P={\frac {RT}{v^{2}}}\left(1-{\frac {c}{vT^{3}}}\right)(v+B)-{\frac {A}{v^{2}}}}

其中

这个方程在密度0.8 ρcr以下时较为精确, 其中 ρcr是物质的临界点密度。 方程中的常数如下表所列： P的单位是kPa, V的单位是 m 3 K m o l {\displaystyle {\frac {m^{3}}{Kmol}}} , R=8.314 k P a . m 3 K m o l . K {\displaystyle {\frac {kPa.m^{3}}{Kmol.K}}}

Benedict–Webb–Rubin 模型

BWR方程

P = R T d + d 2 ( R T ( B + b d ) − − --> ( A + a d − − --> a α α --> d 4 ) − − --> 1 T 2 [ C − − --> c d ( 1 + γ γ --> d 2 ) exp ⁡ ⁡ --> ( − − --> γ γ --> d 2 ) ] ) {\displaystyle P=RTd+d^{2}\left(RT(B+bd)-(A+ad-a{\alpha }d^{4})-{\frac {1}{T^{2}}}[C-cd(1+{\gamma }d^{2})\exp(-{\gamma }d^{2})]\right)}

其中d是摩尔密度； a, b, c, A, B, C, α, γ 是经验常数。

常见气体之范德华常数表

参看

理想气体

理想气体方程式

曹锡章宋天佑等. 无机化学. 高等教育出版社. 1994: 22–25. 

An introduction to thermodynamicsby Y. V. C. Rao

^D. Berthelot in Travaux et Mémoires du Bureau international des Poids et Mesures – Tome XIII (Paris: Gauthier-Villars, 1907)

^Peng, D. Y., and Robinson, D. B. (1976). "A New Two-Constant Equation of State". Industrial and Engineering Chemistry: Fundamentals 15: 59–64. doi:10.1021/i160057a011.

^Gordan J. Van Wylen and Richard E. Sonntage, Fundamental of Classical Thermodynamics, 3rd ed, New York, John Wiley & Sons, 1986 P46 table 3.3

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。