简介

爱因斯坦标记法的基本点子是余向量与向量可以形成标量：

通常会将这写为求和公式形式：

在基底变换之下，标量保持不变。当基底改变时，一个向量的线性变换可以用矩阵来描述，而余向量的线性变换则需用其逆矩阵来描述。这样的设计为的是要保证，不论基底为何，伴随余向量的线性函数（即上述总和）保持不变。由于只有总和不变，而总和所涉及的每一个项目都有可能会改变，所以，爱因斯坦提出了这标记法，重复标号表示总和，不需要用到求和符号：

采用爱因斯坦标记法，余向量都是以下标来标记，而向量都是以上标来标记。标号的位置具有特别意义。请不要将上标与指数混淆在一起，大多数涉及的方程式都是线性，不超过变数的一次方。在方程式里，单独项目内的标号变数最多只会出现两次，假若多于两次，或出现任何其它例外，则都必须特别加以说明，才不会造成含意混淆不清。

向量的表示

在线性代数里，采用爱因斯坦标记法，可以很容易的分辨向量和余向量（又称为1-形式）。向量的分量是用上标来标明，例如，ai{\displaystyle a^{i}\,\!}。给予一个n{\displaystyle n\,\!}维向量空间V{\displaystyle \mathbb {V} \,\!}和其任意基底e=(e1,e2,… … -->,en){\displaystyle \mathbf {e} =(\mathbf {e} _{1},\mathbf {e} _{2},\dots ,\mathbf {e} _{n})\,\!}（可能不是标准正交基），那么，向量a{\displaystyle \mathbf {a} \,\!}表示为

余向量的分量是用下标来标明，例如，α α -->i{\displaystyle \alpha _{i}\,\!}。给予V{\displaystyle \mathbb {V} \,\!}的对偶空间V∗ ∗ -->{\displaystyle \mathbb {V} ^{*}\,\!}和其任意基底ω ω -->=(ω ω -->1,ω ω -->2,… … -->,ω ω -->n){\displaystyle {\boldsymbol {\omega }}=({\boldsymbol {\omega }}^{1},{\boldsymbol {\omega }}^{2},\dots ,{\boldsymbol {\omega }}^{n})\,\!}（可能不是标准正交基），那么，余向量α α -->{\displaystyle {\boldsymbol {\alpha }}\,\!}表示为

采用向量的共变和反变术语，上标表示反变向量（向量）。对于基底的改变，从e{\displaystyle \mathbf {e} \,\!}改变为e¯ ¯ -->{\displaystyle {\overline {\mathbf {e} }}\,\!}，反变向量会变换为

其中，a¯ ¯ -->i{\displaystyle {\overline {a}}^{i}\,\!}是改变基底后的向量的分量，x¯ ¯ -->i{\displaystyle {\overline {x}}^{i}\,\!}是改变基底后的坐标，xj{\displaystyle x^{j}\,\!}是原先的坐标，

下标表示共变向量（余向量）。对于基底的改变，从ω ω -->{\displaystyle {\boldsymbol {\omega }}\,\!}改变为ω ω -->¯ ¯ -->{\displaystyle {\overline {\boldsymbol {\omega }}}\,\!}，共变向量会会变换为

一般运算

矩阵A{\displaystyle A\,\!}的第m{\displaystyle m\,\!}横排，第 n{\displaystyle n\,\!}竖排的元素，以前标记为Amn{\displaystyle A_{mn}\,\!}；现在改标记为Anm{\displaystyle A_{n}^{m}\,\!}。各种一般运算都可以用爱因斯坦标记法来表示如下：

内积

给予向量a{\displaystyle \mathbf {a} \,\!}和余向量α α -->{\displaystyle {\boldsymbol {\alpha }}\,\!}，其向量和余向量的内积为标量：

向量乘以矩阵

给予矩阵A{\displaystyle A\,\!}和向量a{\displaystyle \mathbf {a} \,\!}，它们的乘积是向量b{\displaystyle \mathbf {b} \,\!}：

类似地，矩阵A{\displaystyle A\,\!}的转置矩阵B=AT{\displaystyle B=A^{\mathrm {T} }\,\!}，其与余向量α α -->{\displaystyle {\boldsymbol {\alpha }}\,\!}的乘积是余向量β β -->{\displaystyle {\boldsymbol {\beta }}\,\!}：

矩阵乘法

矩阵乘法表示为

这公式等价于较冗长的普通标记法：

迹

给予一个方块矩阵Aji{\displaystyle A_{j}^{i}\,\!}，总和所有上标与下标相同的元素Aii{\displaystyle A_{i}^{i}\,\!}，可以得到这矩阵的迹t{\displaystyle t\,\!}：

外积

M维向量a{\displaystyle \mathbf {a} \,\!}和N维余向量α α -->{\displaystyle {\boldsymbol {\alpha }}\,\!}的外积是一个M×N矩阵A{\displaystyle A\,\!}：

采用爱因斯坦标记式，上述方程式可以表示为

由于i{\displaystyle i\,\!}和j{\displaystyle j\,\!}代表两个不同的标号，在这案例，值域分别为M和N，外积不会除去这两个标号，而使这两个标号变成了新矩阵A{\displaystyle A\,\!}的标号。

向量的内积

一般力学及工程学会用互相标准正交基的基底向量i^ ^ -->{\displaystyle {\hat {\mathbf {i} }}\,\!}、j^ ^ -->{\displaystyle {\hat {\mathbf {j} }}\,\!}及k^ ^ -->{\displaystyle {\hat {\mathbf {k} }}\,\!}来描述三维空间的向量。

把直角坐标系的基底向量i^ ^ -->{\displaystyle {\hat {\mathbf {i} }}\,\!}、j^ ^ -->{\displaystyle {\hat {\mathbf {j} }}\,\!}及k^ ^ -->{\displaystyle {\hat {\mathbf {k} }}\,\!}写成e^ ^ -->1{\displaystyle {\hat {\mathbf {e} }}_{1}\,\!}、e^ ^ -->2{\displaystyle {\hat {\mathbf {e} }}_{2}\,\!}及e^ ^ -->3{\displaystyle {\hat {\mathbf {e} }}_{3}\,\!}，所以一个向量可以写成：

根据爱因斯坦求和约定，若单项中有标号出现两次且分别位于上标及下标，则此项代表着所有可能值之总和：

由于基底是标准正交基，u{\displaystyle \mathbf {u} \,\!}的每一个分量ui=ui{\displaystyle u^{i}=u_{i}\,\!}，所以，

两个向量u{\displaystyle \mathbf {u} \,\!}与v{\displaystyle \mathbf {v} \,\!}的内积是

由于基底是标准正交基，基底向量相互正交归一：

其中， δ δ -->ij{\displaystyle \ \delta _{ij}\,\!}就是克罗内克函数。当i=j{\displaystyle i=j\,\!}时，则δ δ -->ij=1{\displaystyle \delta _{ij}=1\,\!}，否则δ δ -->ij=0{\displaystyle \delta _{ij}=0\,\!}。

逻辑上，在方程式内的任意项目，若遇到了克罗内克函数 δ δ -->ij{\displaystyle \ \delta _{ij}\,\!}，就可以把方程式中的标号i{\displaystyle i\,\!}转为j{\displaystyle j\,\!}或者把标号j{\displaystyle j\,\!}转为i{\displaystyle i\,\!}。所以，

向量的叉积

采用同样的标准正交基e^ ^ -->1{\displaystyle {\hat {\mathbf {e} }}_{1}\,\!}、e^ ^ -->2{\displaystyle {\hat {\mathbf {e} }}_{2}\,\!}及e^ ^ -->3{\displaystyle {\hat {\mathbf {e} }}_{3}\,\!}，两个向量u{\displaystyle \mathbf {u} \,\!}与v{\displaystyle \mathbf {v} \,\!}的叉积，以方程式表示为

注意到

其中，张量 ϵ ϵ -->ijk{\displaystyle \ \epsilon _{ijk}\,\列维-奇维塔符号塔符号，定义为

所以，

设定w=u× × -->v{\displaystyle \mathbf {w} =\mathbf {u} \times \mathbf {v} \,\!}，那么，

所以，

向量的共变分量和反变分量

在欧几里得空间V{\displaystyle \mathbb {V} \,\!}里，共变向量和反变向量之间的区分很小。这是因为能够使用内积运算从向量求得余向量；对于所有向量b{\displaystyle \mathbf {b} \,\!}，通过下述方程式，向量a{\displaystyle \mathbf {a} \,\!}唯一地确定了余向量α α -->{\displaystyle {\boldsymbol {\alpha }}\,\!}：

逆过来，通过上述方程式，每一个余向量α α -->{\displaystyle {\boldsymbol {\alpha }}\,\!}唯一地确定了向量a{\displaystyle \mathbf {a} \,\!}。由于这向量与余向量的相互辨认，我们可以提到向量的共变分量和反变分量；也就是说，它们只是同样向量对于基底和其对偶基底的不同表现。

给予V{\displaystyle \mathbb {V} \,\!}的一个基底f=(X1,X2,… … -->,Xn){\displaystyle {\mathfrak {f}}=(X_{1},X_{2},\dots ,X_{n})\,\!}，则必存在一个唯一的对偶基底f♯ ♯ -->=(Y1,Y2,… … -->,Yn){\displaystyle {\mathfrak {f}}^{\sharp }=(Y^{1},Y^{2},\dots ,Y^{n})\,\!}，满足

其中，张量δ δ -->ji{\displaystyle \delta _{j}^{i}\,\!}是克罗内克函数。

以这两种基底，任意向量a{\displaystyle \mathbf {a} \,\!}可以写为两种形式

其中，ai[f]{\displaystyle a^{i}[{\mathfrak {f}}]\,\!}是向量a{\displaystyle \mathbf {a} \,\!}对于基底f{\displaystyle {\mathfrak {f}}\,\!}的反变分量，ai[f]{\displaystyle a_{i}[{\mathfrak {f}}]\,\!}是向量v{\displaystyle \mathbf {v} \,\!}对于基底f{\displaystyle {\mathfrak {f}}\,\!}的共变分量，

欧几里得空间

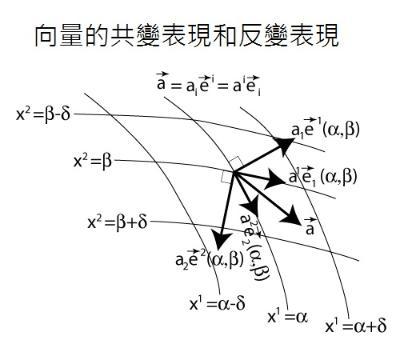
将向量a{\displaystyle \mathbf {a} \,\!}投影于坐标轴ei{\displaystyle \mathbf {e} ^{i}\,\!}，可以求得其反变分量ai{\displaystyle a^{i}\,\!}；将向量a{\displaystyle \mathbf {a} \,\!}投影于坐标曲面的法线ei{\displaystyle \mathbf {e} _{i}\,\!}，可以求得其共变分量ai{\displaystyle a_{i}\,\!}。

在欧几里得空间R3{\displaystyle \mathbb {R} ^{3}\,\!}里，使用内积运算，能够从向量求得余向量。给予一个可能不是标准正交基的基底，其基底向量为e1{\displaystyle \mathbf {e} _{1}\,\!}、e2{\displaystyle \mathbf {e} _{2}\,\!}、e3{\displaystyle \mathbf {e} _{3}\,\!}，就可以计算其对偶基底的基底向量：

其中，τ τ -->=e1⋅ ⋅ -->(e2× × -->e3){\displaystyle \tau =\mathbf {e} _{1}\cdot (\mathbf {e} _{2}\times \mathbf {e} _{3})\,\!}是基底向量e1{\displaystyle \mathbf {e} _{1}\,\!}、e2{\displaystyle \mathbf {e} _{2}\,\!}、e3{\displaystyle \mathbf {e} _{3}\,\!}共同形成的平行六面体的体积。

反过来计算，

其中，τ τ -->′=e1⋅ ⋅ -->(e2× × -->e3)=1/τ τ -->{\displaystyle \tau "=\mathbf {e} ^{1}\cdot (\mathbf {e} ^{2}\times \mathbf {e} ^{3})=1/\tau \,\!}是基底向量e1{\displaystyle \mathbf {e} ^{1}\,\!}、e2{\displaystyle \mathbf {e} ^{2}\,\!}、e3{\displaystyle \mathbf {e} ^{3}\,\!}共同形成的平行六面体的体积。

虽然ei{\displaystyle \mathbf {e} _{i}\,\!}与ej{\displaystyle \mathbf {e} ^{j}\,\!}并不相互标准正交，它们相互对偶：

虽然ei{\displaystyle \mathbf {e} ^{i}\,\!}与ej{\displaystyle \mathbf {e} _{j}\,\!}并不相互标准正交，它们相互对偶：

这样，任意向量a{\displaystyle \mathbf {a} \,\!}的反变分量为

类似地，共变分量为

这样，a{\displaystyle \mathbf {a} \,\!}可以表示为

或者，

综合上述关系式，

向量a{\displaystyle \mathbf {a} \,\!}的共变分量为

其中，gji=ej⋅ ⋅ -->ei{\displaystyle g_{ji}=\mathbf {e} _{j}\cdot \mathbf {e} _{i}\,\!}是度规张量。

向量a{\displaystyle \mathbf {a} \,\!}的反变分量为

其中，gji=ej⋅ ⋅ -->ei{\displaystyle g^{ji}=\mathbf {e} ^{j}\cdot \mathbf {e} ^{i}\,\!}是共轭度规张量。

共变分量的标号是下标，反变分量的标号是上标。假若共变基底向量组成的基底是标准正交基，或反变基底向量组成的基底是标准正交基，则共变基底与反变基底相互等价。那么，就没有必要分辨共变分量和反变分量，所有的标号都可以用下标来标记。

抽象定义

思考维度为n{\displaystyle n\,\!}的向量空间V{\displaystyle \mathbb {V} \,\!}。给予一个可能不是标准正交基的基底(e1,e2,… … -->,en){\displaystyle (\mathbf {e} _{1},\mathbf {e} _{2},\dots ,\mathbf {e} _{n})\,\!}。那么，在V{\displaystyle \mathbb {V} \,\!}内的向量v{\displaystyle \mathbf {v} \,\!}，对于这基底，其分量为v1{\displaystyle v^{1}\,\!}、v2{\displaystyle v^{2}\,\!}、...vn{\displaystyle v^{n}\,\!}。以方程式表示，

在这方程式右手边，标号i{\displaystyle i\,\!}在同一项目出现了两次，一次是上标，一次是下标，因此，从i{\displaystyle i\,\!}等于1{\displaystyle 1\,\!}到n{\displaystyle n\,\!}，这项目的每一个可能值都必须总和在一起。

爱因斯坦约定的优点是，它可以应用于从V{\displaystyle \mathbb {V} \,\!}用张量积和对偶性建立的向量空间。例如，V⊗ ⊗ -->V{\displaystyle \mathbb {V} \otimes \mathbb {V} \,\!}，V{\displaystyle \mathbb {V} \,\!}与自己的张量积，拥有由形式为eij=ei⊗ ⊗ -->ej{\displaystyle \mathbf {e} _{ij}=\mathbf {e} _{i}\otimes \mathbf {e} _{j}\,\!}的张量组成的基底。任意在V⊗ ⊗ -->V{\displaystyle \mathbb {V} \otimes \mathbb {V} \,\!}内的张量T{\displaystyle \mathbf {T} \,\!}可以写为

向量空间V{\displaystyle \mathbb {V} \,\!}的对偶空间V∗ ∗ -->{\displaystyle \mathbb {V} ^{*}\,\!}拥有基底(e1,e2,… … -->,en){\displaystyle (\mathbf {e} ^{1},\mathbf {e} ^{2},\dots ,\mathbf {e} ^{n})\,\!}，遵守规则

其中，δ δ -->ji{\displaystyle \delta _{j}^{i}\,\!}是克罗内克函数。

范例

为了更明确地解释爱因斯坦求和约定，在这里给出几个简单的例子。

思考四维时空，标号的值是从0到3。两个张量，经过张量缩并（tensor contraction）运算后，变为一个标量：

方程式的右手边有两个项目：

思考在黎曼空间的弧线元素长度ds{\displaystyle ds\,\!}：

参阅

狄拉克标记

抽象指标记号

潘洛斯图形标记法（Penrose graphical notation）

参考文献

Kuptsov, L.P.,Einstein rule, (编) Hazewinkel, Michiel,数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 .

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。