数学性质

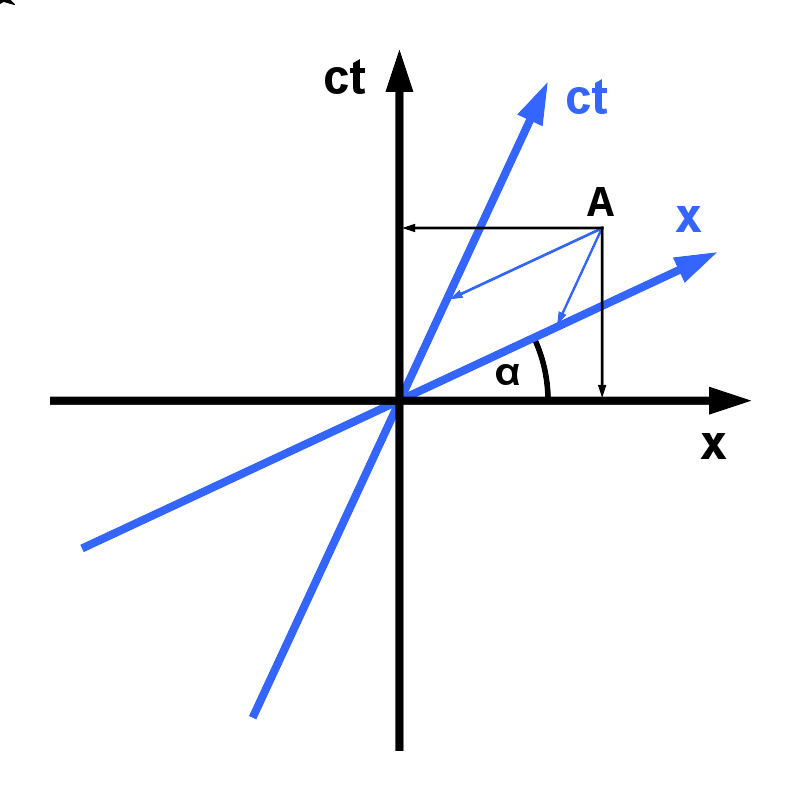
在闵可夫斯基时空里，不同惯性参考系的坐标轴

在闵可夫斯基时空内的任何一点，都可以用四维矢量（一组标准基底的四个坐标） x μ μ --> = ( x 0 , x 1 , x 2 , x 3 ) {\displaystyle {x}^{\mu }=({x}^{0},\,{x}^{1},\,{x}^{2},\,{x}^{3})} 来表示；其中，上标 μ μ --> = 0 , 1 , 2 , 3 {\displaystyle \mu =0,\,1,\,2,\,3} 标记时空的维数次序。称这四维矢量为“坐标四维矢量”，又称“四维坐标”，定义为

其中， c {\displaystyle c} 是光速， t {\displaystyle t} 是时间， ( x , y , z ) {\displaystyle (x,\,y,\,z)} 是位置的三维直角坐标。

为了确使每一个坐标的单位都是长度单位，定义 x 0 = d e f c t {\displaystyle {x}^{0}\ {\stackrel {def}{=}}\ ct} 。

“四维位移”定义为两个事件之间的矢量差。在时空图里，四维位移可以用从第一个事件指到第二个事件的箭矢来表示。当矢量的尾部是坐标系的原点时，位移就是位置。四维位移 Δ Δ --> x μ μ --> {\displaystyle \Delta {x}^{\mu }} 表示为

带有上标的四维矢量 U μ μ --> {\displaystyle {U}^{\mu }} 称为反变矢量，其分量标记为

假若，标号是下标，则称四维矢量 U μ μ --> {\displaystyle {U}_{\mu }} 为协变矢量。其分量标记为

在这里，闵可夫斯基度规 η η --> μ μ --> ν ν --> {\displaystyle \eta _{\mu \nu }} 被设定为

采用爱因斯坦求和约定，则四维矢量的协变坐标和反变坐标之间的关系为

闵可夫斯基度规与它的“共轭度规张量” η η --> μ μ --> ν ν --> {\displaystyle \eta ^{\mu \nu }} 相等：

洛伦兹变换

给予两个惯性参考系 S {\displaystyle {\mathcal {S}}} 、 S ¯ ¯ --> {\displaystyle {\bar {\mathcal {S}}}} ；相对于参考系 S {\displaystyle {\mathcal {S}}} ，参考系 S ¯ ¯ --> {\displaystyle {\bar {\mathcal {S}}}} 以速度 v = v x ^ ^ --> {\displaystyle \mathbf {v} =v{\hat {\mathbf {x} }}} 移动。对于这两个参考系，相关的“洛伦兹变换矩阵” Λ Λ --> μ μ --> ν ν --> {\displaystyle \Lambda ^{\mu }{}_{\nu }} 是

其中， γ γ --> = 1 1 − − --> ( v c ) 2 {\displaystyle \gamma ={\cfrac {1}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}洛伦兹因子是洛伦兹因子， β β --> = v c {\displaystyle \beta ={\frac {v}{c}}} 是“贝塔因子”。

对于这两个参考系 S {\displaystyle {\mathcal {S}}} 、 S ¯ ¯ --> {\displaystyle {\bar {\mathcal {S}}}} ，假设一个事件的四维坐标分别为 x μ μ --> {\displaystyle {x}^{\mu }} 、 x ¯ ¯ --> μ μ --> {\displaystyle {\bar {x}}^{\mu }} 。那么，这两个四维坐标之间的关系为

其中， Λ Λ --> ¯ ¯ --> μ μ --> ν ν --> {\displaystyle {\bar {\Lambda }}^{\mu }{}_{\nu }} 是 Λ Λ --> μ μ --> ν ν --> {\displaystyle \Lambda ^{\mu }{}_{\nu }} 的逆反，

将这两个四维坐标之间的关系式合并为一，则可得到

因此，可以找到洛伦兹变换矩阵的一个特性：

其中， δ δ --> μ μ --> ξ ξ --> {\displaystyle \delta ^{\mu }{}_{\xi }} 是克罗内克函数。

另外一个很有用的特性为

给定一个事件在某惯性参考系的四维坐标，通过洛伦兹变换，就可计算出这事件在另外一个惯性参考系的四维坐标。这是个很有用的物理性质。当研究物理现象时，所涉及的四维矢量，最好都能够具有这有用的性质。这样，可以使得数学分析更加精致犀利。以方程表示，对于两个参考系 S {\displaystyle {\mathcal {S}}} 、 S ¯ ¯ --> {\displaystyle {\bar {\mathcal {S}}}} ，具有这种有用性质的四维矢量 U μ μ --> {\displaystyle {U}^{\mu }} 、 U ¯ ¯ --> μ μ --> {\displaystyle {\bar {U}}^{\mu }} 满足

在计算这四维矢量对于时间的导数时，若能选择固有时为时间变数，则求得的四维矢量仍旧具有这有用的性质。因为，固有时乃是个不变量；改变惯性参考系不会改变不变量。

假设一个物体运动于闵可夫斯基时空。在“实验室参考系”里，物体运动的速度随着时间改变。对于每瞬时刻，选择与物体同样运动的惯性参考系，称为“瞬间共动参考系”（momentarily comoving reference frame）。在这瞬间共动参考系里，物体的速度为零，因此，这参考系也是物体的“瞬间静止参考系”。随着物体不断地改变运动速度与方向，新的惯性参考系也会不断地改换为瞬间共动参考系。 随着这些不断改换的瞬间同行坐标系所测得的时间即为固有时，标记为 τ τ --> {\displaystyle \tau } 。这就好像给物体挂戴一只手表，随着物体的运动，手表也会做同样的运动，而手表所纪录的时间就是固有时。

这物体的运动可以用一条世界线 x ( τ τ --> ) {\displaystyle x(\tau )} 来描述时间膨胀间膨胀，发生于物体的两个本地事件的微小固有时间隔 Δ Δ --> τ τ --> {\displaystyle \Delta \tau } 与从别的惯性参考系 S {\displaystyle {\mathcal {S}}} 所观测到的微小时间间隔 Δ Δ --> t {\displaystyle \Delta t} 的关系为

所以，固有时 τ τ --> {\displaystyle \tau } 对于其它时间 t {\displaystyle t} 的导数为

闵可夫斯基内积

在闵可夫斯基空间里，两个四维矢量 U μ μ --> {\displaystyle U^{\mu }} 与 V μ μ --> {\displaystyle V_{\mu }} 的内积，称为 闵可夫斯基内积 ，以方程表示为：

由于这内积并不具正定性，即

可能会是负数；而欧几里得内积一定不是负数。

许多学者喜欢使用相反正负号的 η η --> {\displaystyle \eta } ：

这样， U μ μ --> {\displaystyle U^{\mu }} 与 V μ μ --> {\displaystyle V_{\mu }} 的内积改变为

其它相联的量值也会因而改变正负号，但这不会改变系统的物理性质。

从参考系 S {\displaystyle {\mathcal {S}}} 改换至另一参考系 S ¯ ¯ --> {\displaystyle {\overline {\mathcal {S}}}} ， U μ μ --> {\displaystyle U^{\mu }} 与 V μ μ --> {\displaystyle V_{\mu }} 的内积为

所以，在闵可夫斯基时空内，两个四维矢量的内积是个不变量：

四维矢量可以分类为 类时 ， 类空 ，或 类光 （ 零矢量 ）：

动力学实例

四维速度

设想一个物体运动于闵可夫斯基时空，则其世界线的任意事件 x μ μ --> ( τ τ --> ) {\displaystyle x^{\mu }(\tau )} 的四维速度 U μ μ --> {\displaystyle U^{\mu }} 定义为

其中， u = ( d x 1 d t , d x 2 d t , d x 3 d t ) {\displaystyle \mathbf {u} =\left({\frac {\mathrm {d} x^{1}}{\mathrm {d} t}},\,{\frac {\mathrm {d} x^{2}}{\mathrm {d} t}},\,{\frac {\mathrm {d} x^{3}}{\mathrm {d} t}}\right)} 是三维速度，或经典速度矢量。

U μ μ --> {\displaystyle U^{\mu }} 的空间部分与经典速度 u {\displaystyle \mathbf {u} } 的关系为

四维速度与自己的内积等于光速平方，是一个不变量：

在物体的瞬间共动参考系里，物体的速度为零，因此，四维速度为

其方向与瞬间共动参考系的第零个基底矢量 e ^ ^ --> 0 = ( 1 , 0 , 0 , 0 ) M C R F {\displaystyle {\hat {\mathbf {e} }}_{0}=\left(1,0,0,0\right)_{MCRF}} 同向；

其中， M C R F {\displaystyle MCRF} 表示从瞬间共动参考系观察得到的数据。

四维加速度

四维加速度 α α --> μ μ --> {\displaystyle \alpha ^{\mu }} 定义为

经过一番运算，可以得到洛伦兹因子对于时间的导数：

其中， a = d u d t {\displaystyle \mathbf {a} ={\frac {\mathrm {d} \mathbf {u} }{\mathrm {d} t}}} 是经典加速度。

所以，四维加速度 α α --> μ μ --> {\displaystyle \alpha ^{\mu }} 可以表示为

由于 U μ μ --> U μ μ --> {\displaystyle U_{\mu }U^{\mu }} 是个常数，四维加速度与四维速度相互正交；也就是说，四维速度与四维加速度的闵可夫斯基内积等于零：

对于每一条世界线，这计算结果都成立。

注意到在瞬间共动参考系里， U μ μ --> {\displaystyle U_{\mu }} 只有时间分量不等与零，所以， α α --> μ μ --> {\displaystyle \alpha ^{\mu }} 为的时间分量为零：

四维动量

一个静止质量为 m {\displaystyle m} 的粒子的四维动量 P μ μ --> {\displaystyle P^{\mu }} 定义为

经典动量 p {\displaystyle \mathbf {p} } 定义为

其中， m r e l {\displaystyle m_{rel}} 是相对论性质量。

所以， P μ μ --> {\displaystyle P^{\mu }} 的空间部分等于经典动量 p {\displaystyle \mathbf {p} } ：

四维力

作用于粒子的四维力定义为粒子的四维动量对于固有时的导数：

提出四维动量内的静止质量因子，即可发觉四维力就是静止质量乘以四维加速度：

因此，四维力可以表示为

经典力 f {\displaystyle \mathbf {f} } 定义为

所以， F μ μ --> {\displaystyle F^{\mu }} 的空间部分等于 γ γ --> f {\displaystyle \gamma \mathbf {f} } ：

物理内涵

在四维矢量的表述里，存在着许多能量与物质之间的关系。从这些特别关系，可以显示出这表述的功能与精致。

质能方程

假设，在微小时间间隔 d t {\displaystyle \mathrm {d} t} ，一个运动于时空的粒子，感受到作用力 f {\displaystyle \mathbf {f} } 的施加，而这粒子的微小位移为 d x {\displaystyle \mathrm {d} \mathbf {x} } 。那么，作用力 f {\displaystyle \mathbf {f} } 对于这粒子所做的微小机械功 d W {\displaystyle \mathrm {d} W} 为

因此，这粒子的动能的改变 d K {\displaystyle \mathrm {d} K} 为

粒子的动能 K {\displaystyle K} 对于时间的导数为

将前面经典力和经典速度的公式带入，可以得到

这公式的反微分为

当粒子静止时，动能等于零。所以，

这公式的右手边第二个项目就是静止能量 E 0 = d e f m c 2 {\displaystyle E_{0}\ {\stackrel {def}{=}}\ mc^{2}} 。动能 K {\displaystyle K} 加上静止能量 E 0 {\displaystyle E_{0}} 等于总能量 E {\displaystyle E} ：

再加简化，以相对论性质量 m r e l {\displaystyle m_{rel}} 表示：

这方程称为质能方程。

能量-动量关系式

使用质能方程 E = m r e l c 2 = γ γ --> m c 2 {\displaystyle E=m_{rel}c^{2}=\gamma mc^{2}} ，四维动量可以表示为

四维动量与自己的内积为

改以四维速度来计算内积：

所以，能量-动量关系式为

电磁学实例

四维电流密度

在电磁学里，四维电流密度 J μ μ --> {\displaystyle J^{\mu }} 是一个四维矢量，定义为

其中， ρ ρ --> {\displaystyle \rho } 是电荷密度， j {\displaystyle \mathbf {j} } 是三维电流密度。

在瞬间共动参考系所观测到的电荷密度，称为 固有电荷密度 ρ ρ --> 0 = ρ ρ --> / γ γ --> {\displaystyle \rho _{0}=\rho /\gamma } 。四维电流密度与四维速度的关系为

电荷守恒定律能以三维矢量表示为

这定律也能以四维电流密度表示为

从这方程，可以推论四维电流密度的四维散度等于零。

电磁四维势

电磁四维势是由电势 ϕ ϕ --> {\displaystyle \phi \,} 与矢量势 A {\displaystyle \mathbf {A} } 共同形成的，定义为

黎曼-索末菲方程 表示电磁四维势与四维电流密度之间的关系 ：

其中， μ μ --> 0 {\displaystyle \mu _{0}} 是磁常数， ◻ ◻ --> = ∂ ∂ --> 2 = ∂ ∂ --> α α --> ∂ ∂ --> α α --> = ( 1 c 2 ∂ ∂ --> 2 ∂ ∂ --> t 2 − − --> ∇ ∇ --> 2 ) {\displaystyle \Box =\partial ^{2}=\partial _{\alpha }\partial ^{\alpha }=\left({\frac {1}{c^{2}}}\ {\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}\right)} 是达朗贝尔算符，又称为四维拉普拉斯算符。

四维频率和四维波矢量

一个平面电磁波的四维频率 ν ν --> μ μ --> {\displaystyle {\nu }^{\mu }} 定义为

其中， f {\displaystyle f} 是电磁波的频率， n {\displaystyle \mathbf {n} } 是朝着电磁波传播方向的单位矢量。

四维频率与自己的内积永远等于零：

一个近单色光的波包的波动性质可以用四维波矢量 K α α --> {\displaystyle {K}^{\alpha }} 来描述：

其中， k {\displaystyle \mathbf {k} } 是三维波矢量。

四维波矢量与四维频率之间的关系为

参阅

洛仑兹协变性

参考文献

Griffiths, David J. Introduction to Electrodynamics (3rd ed.). Prentice Hall. 1998: pp. 477–543. ISBN 0-13-805326-X. 引文格式1维护：冗余文本 (link)

Rindler, W. Introduction to Special Relativity (2nd edition). Clarendon Press Oxford. 1991. ISBN 0-19-853952-5.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。