物质波相速度

量子力学中，粒子也具有波的行为，并带有复数相位。透过德布罗意假说，我们可以得到：

运用相对论中能量与动量的关系式：

其中Ek{\displaystyle E_{k}}是粒子总能（运动学观点上，即静质能加上动能），p是粒子动量，γ γ -->{\displaystyle \gamma洛伦兹因子兹因子，c是光速，以及β β -->{\displaystyle \beta }是速度与c的比值。变数v可以是粒子速度或相应的物质波群速度。细节请参阅群速度条目。既然根据狭义相对论，带质量粒子的速度v<c{\displaystyle v必然成立，因此相速度永远大于c，即：

并且可以看到当粒子速度在相对论性范围，相速度趋近于c。超光速的相速度并不违反狭义相对论，因其并不带有任何信息的传递。细节请参阅讯号速度条目。

与群速度相异

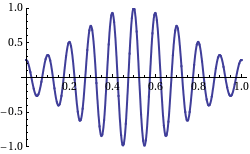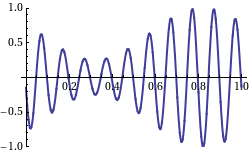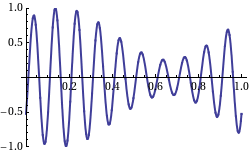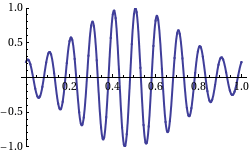
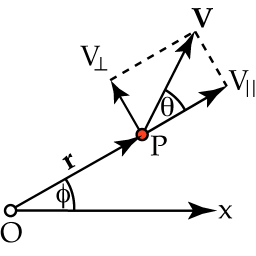
群速度与相速度

群速度迥异于“相速度”的概念是首先由哈密顿于1839年提出，这方面完整的处理则出现在瑞利勋爵（Lord Rayleigh）的1877年的著作《声理论》（Theory of Sound）中。

（英文）Group and Phase Velocity- Java applet显示群速度与相速度的差异。

文献

莱昂·布里渊《波传递与群速度》（Wave Propagation and Group Velocity）Academic Press Inc., New York（1960年）ISBN 0-1213-4968-3

Tipler, Paul A. and Ralph A. Llewellyn (2003). Modern Physics. 4th ed. New York; W. H. Freeman and Company. ISBN 0-7167-4345-0. 222-3 pp.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。