概论

将五维时空分开成四维的爱因斯坦方程以及麦克斯韦方程组是首先由 古纳尔·诺德斯特诺姆 （ 英语 ： Gunnar Nordström ） （Gunnar Nordström）于1914年所发现，出现在他的引力理论内文中，但随后就被世人遗忘。在1926年，奥斯卡·克莱因（Oskar Klein）提议了第四个空间维度卷曲成一个半径非常小的圆，所以粒子沿着这个轴移动很短的距离，就会回到起始点。粒子在回到起始点前所能行进的距离则称作是该维度的大小。这个 额外维度 （extra dimension）是一个紧集，而时空具有紧致维度的现象则称作是紧化。

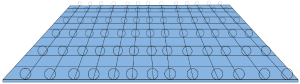
第五维度卷曲成圆，构成了最早的高维宇宙模型。此模型仅多出现了一个额外维度。

现代几何学中，额外的第五维度可以被理解为圆群U(1) ，而基本上，电磁学可以用在纤维丛上规范群 U （1）的规范场论来诠释。一旦这样的几何诠释能被理解，则将 U （1）换成广义的李群就显得容易而直观。这样的推广常称作是杨-米尔斯理论。若要提到两者的差异，则可说杨–米尔斯理论是在平坦时空的场合处理，而卡鲁扎-克莱因理论则是在更具一般性的弯曲时空中处理。卡鲁扎-克莱因理论的底空间不一定是四维时空，而可以是任何的（伪）黎曼流形，或者甚至是超对称流形、轨形或非交换空间。

时间-空间-物质理论

卡鲁扎-克莱因理论的一个特别的变形是所谓的 时间-空间-物质理论 （ space-time-matter theory ）或称 引生物质理论 （ induced matter theory ），主要是由Paul Wesson及其他人所推广，他们组成所谓的Space-Time-Matter Consortium。在这理论版本中，值得注意的是下面方程所得的解：

其中 R A B {\displaystyle R_{AB}} 是五维里奇曲率，也可以在四维中重新表述，这样的解满足爱因斯坦方程：

其中 T μ μ --> ν ν --> {\displaystyle T_{\mu \nu }} 的精准形式来自于五维空间中的里奇平坦条件（Ricci-flat condition）。既然能量-动量张量 T μ μ --> ν ν --> {\displaystyle T_{\mu \nu }} 常被了解为四维空间中的物质密度，上面的结果则被诠释成：四维物质是引生自五维空间中的几何。

特别是 R A B = 0 {\displaystyle R_{AB}=0} 的孤立子（soliton）解可被展示：其包含了辐射主导形式（早期宇宙）与物质主导形式（晚期宇宙）中的罗伯逊-沃尔克度规（Robertson-Walker metric）。一般方程则可被展示与经典范畴的引力理论测试相符，在物理学原则上可以被接受，而其仍留有相当多的自由度可提供一些有趣的宇宙学模型。

几何诠释

相关条目

经典引力理论

DGP模型

超引力

紧致化

卡拉比-丘流形

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。