几何学与拓扑学结构

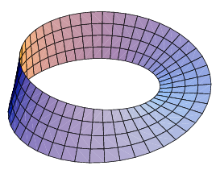
用Matlab描绘的莫比乌斯带

一个利用参数方程式创造出立体莫比乌斯带的方法：

这个方程组可以创造一个边长为1半径为1的莫比乌斯带，所处位置为x-y面，中心为（0，0，0）。参数u在v从一个边移动到另一边的时候环绕整个带子。

如果用圆柱坐标系（r,θ,z）表示的话，一个无边界的莫比乌斯带可以表示为：

从拓扑学上来讲，莫比乌斯带可以定义为矩阵[0,1]×[0,1]，边由在0 ≤ x ≤ 1的时候（x,0）~（1-x,1）决定，如右图所示。

莫比乌斯带是一个二维的紧致流形（即一个有边界的面），可以嵌入到三维或更高维的流形中。它是一个不可定向的的标准范例，可以看作RP # RP。同时也是数学上描绘纤维丛的例子之一。特别地，它是一个有一纤维单位区间，I = [0,1]的圆S上的非平凡丛。仅从莫比乌斯带的边缘看去给出S上一个非平凡的两个点（或Z2）的从。

有关的物体

和莫比乌斯带非常近似的一个几何学物体叫做克莱因瓶。一个克莱因瓶可以用粘贴两个莫比乌斯带的方法制作出来。但是如果物体不进行自我交叉，这个步骤在三维空间内是不可能完成的。

另外一个相近的结构是实射影平面。如果在实射影平面上有一个洞的话，从左侧看就会形成一个莫比乌斯带。或者把莫比乌斯带的边界进行有限定义，就会形成一个真投影屏面。更形象地说法是重建莫比乌斯带的边缘形成一个普通的环。有一种普遍的误解认为如果不进行平面的自我交叉就无法在三维空间内形成一个有普通环边缘的莫比乌斯带。事实上是可能的，方法是这样的：定义C为xy面上的单位圆，现在连接C上面的对跖点，比如θ和θ + π。当θ在0到π/2之间运动的时候，在xy面上方做这条线的反余切，其他情况则在面下做反余切。

艺术和科技

莫比乌斯带为很多艺术家提供了灵感，比如美术家莫里茨·科内利斯·埃舍尔就是一个利用这个结构在他木刻画作品里面的人，最著名的就是莫比乌斯二代，图画中表现一些蚂蚁在莫比乌斯带上面前行。

它也经常出现在科幻小说里面，比如亚瑟·克拉克的《黑暗之墙》。科幻小说常常想象我们的宇宙就是一个莫比乌斯带。由A.J.Deutsch创作的短篇小说《一个叫莫比乌斯的地铁站》为波士顿地铁站创造了一个新的行驶线路，整个线路按照莫比乌斯带方式扭曲，走入这个线路的火车都消失不见。另外一部小说《星际迷航：下一代》中也用到了莫比乌斯带空间的概念。

有一首小诗也描写了莫比乌斯带：

莫比乌斯带也被用于工业制造。一种从莫比乌斯带得到灵感的传送带能使用更长的时间，因为可以更好的利用整个带子，或者用于制造磁带，可以承载双倍的信息量。

有一座钢制的莫比乌斯带雕塑位于美国华盛顿的史密斯森林历史和技术博物馆。

荷兰建筑师Ben Van Berkel以莫比乌斯带为创作模型设计了著名的莫比乌斯住宅。

在日本漫画《哆啦A梦》中，哆啦A梦有个道具的外观就是莫比乌斯带；在故事中，只要将这个环套在门把上，则外面的人进来之后，看到的依然是外面。

在电玩游戏“音速小子－滑板流星故事”中最后一关魔王战就是在莫比乌斯带形状的跑道上进行，如果不打败魔王，就会一直在莫比乌斯带上无限循环的跑下去。

1988年在日本上映的动画电影机动战士高达 逆袭的夏亚以莫比乌斯带作为对命运的隐喻：人类就好比行走在莫比乌斯带上的蚂蚁一般，永远逃不出这个怪圈，不断重复着相同的错误，类同的悲剧也在不断地上演。

电影的主题歌BEYOND THE TIME（メビウスの宇宙を越えて）亦呼应了这个主题（日文“メビウス”就是Möbius的意思）。

jojo奇妙旅程第6部空条徐伦对c-moon一幕亦有于战斗中使用此结构。

韩国导演金基德2013年的电影《莫比乌斯》命名就取材于莫比乌斯环，象征人性周而复始的重复悲剧和错误。

网络上流传一部动画影片，用莫比乌斯带原理，来解释巴哈所著的逆行卡农作品。

《Bilibili拜年祭2017》中作品《再一次》以莫比乌斯带原理构筑了困住木琳与海阅的古堡。

参见

克莱因瓶

三叶结

潘洛斯三角

分子结

参考资料

《数学趣闻集锦》，上海教育出版社出版，美国T·帕帕斯著，中国张远南、张永译，ISBN 7-5320-6052-7

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。