符号史

正割的数学符号为sec，出自英文secant。该符号最早由数学家吉拉德在他的著作《三角学》中所用。

定义

直角三角形中

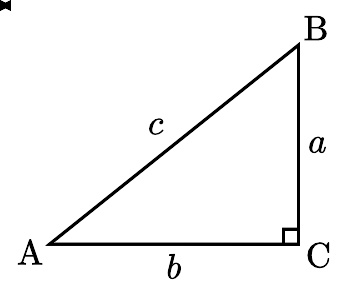
直角三角形，∠C为直角，∠A 的角度为 θ θ --> {\displaystyle \theta } ， 对于 ∠A 而言，a为对边、b为邻边、c为斜边

在直角三角形中，一个锐角 ∠A 的 正割 定义为它的斜边与邻边的比值，也就是：

直角坐标系中

设α是平面直角坐标系xOy中的一个象限角， P ( x , y ) {\displaystyle P\left({x,y}\right)} 是角的终边上一点， r = x 2 + y 2 > 0 {\displaystyle r={\sqrt {x^{2}+y^{2}}}>0} 是距离原点O的距离，则α的正割定义为：

单位圆定义

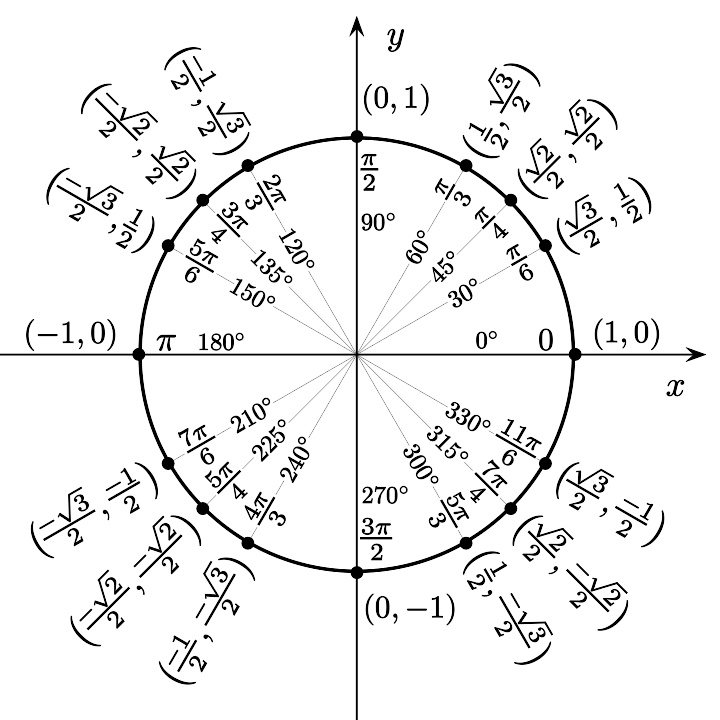
单位圆

图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线，同 x 轴正半部分得到一个角θ，并与单位圆相交。这个交点的 y 坐标等于sin θ。在这个图形中的三角形确保了这个公式；半径等于斜边并有长度1，所以有了sec θ = 1/ x 。单位圆可以被认为是通过改变邻边和对边的长度并保持斜边等于1查看无限数目的三角形的一种方式。

对于大于2π或小于−2π的角度，简单的继续绕单位圆旋转。在这种方式下，正割变成了周期为2π的周期函数：

对于任何角度θ和任何整数 k 。

与其他函数定义

正割函数和余弦函数互为倒数

即：

级数定义

正割也能使用泰勒级数来定义：

微分方程定义

sec的微分是sec和tan的乘积

sec的导数如下：

sec ′ ⁡ ⁡ --> x = sec ⁡ ⁡ --> x tan ⁡ ⁡ --> x {\displaystyle \sec "x\ =\sec x\tan x}

sec ″ ⁡ ⁡ --> x = sec 3 ⁡ ⁡ --> x + sec ⁡ ⁡ --> x tan 2 ⁡ ⁡ --> x {\displaystyle \sec ""x\ =\sec ^{3}x+\sec x\tan ^{2}x}

sec ‴ ⁡ ⁡ --> x = 5 sec 3 ⁡ ⁡ --> x tan ⁡ ⁡ --> x + sec ⁡ ⁡ --> x tan 3 ⁡ ⁡ --> x {\displaystyle \sec """x\ =5\sec ^{3}x\tan x+\sec x\tan ^{3}x}

sec ⁗ ⁡ ⁡ --> x = 5 sec 5 ⁡ ⁡ --> x + 18 sec 3 ⁡ ⁡ --> x tan 2 ⁡ ⁡ --> x + sec ⁡ ⁡ --> x tan 4 ⁡ ⁡ --> x {\displaystyle \sec """"x\ =5\sec ^{5}x+18\sec ^{3}x\tan ^{2}x+\sec x\tan ^{4}x}

另外

所以微分方程定义为：

指数定义

sec ⁡ ⁡ --> θ θ --> = 2 e i θ θ --> + e − − --> i θ θ --> {\displaystyle \sec \theta ={\frac {2}{e^{{\mathrm {i} }\theta }+e^{-{\mathrm {i} }\theta }}}\,}

恒等式

和差角公式

巴洛的正割积分

巴洛在1670年提出正割的积分

正割定理

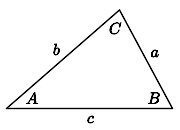
一个三角形。它的三个内角及其对边。

有一些含有正割的恒等式，满足任意三角形ABC：

这些实际上是射影定理的倒数。

参见

余割

余弦

正弦

正切

三角函数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。