正五边形

正五边形 是指五个边等长且五个角等角的五边形，其内角为108度，是一种正多边形，在施莱夫利符号中可以用 { 5 } {\displaystyle \left\{5\right\}} 来表示。

正五边形的中心角为72度，其具有五个对称轴，其旋转对称性有5个阶（72°、144°、216° 和 288°）。

其中R为外接圆半径。

边长为t的正凸五边形面积可以将之分割成5个等腰三角形计算：

正五边形不能镶嵌平面，因为其内角是108°，不能整除360°。截至2015年 ( 2015-Missing required parameter 1= month ! ) ，已知有15种凸五边形镶嵌平面，还未知道是否尚有其他的凸五边形 。

面积公式推导

正多边形的面积公式为：

其中， P 是周长、 r 是边心距。正五边形的 P 和 r 可由三角函数计算：

其中， t 是正五边形的边长。

内切圆半径

正五边形是一个圆外切多边形，因此有内切圆。其内切圆半径与边心距相同，并且可以尤其边长来决定。

其中，r为内切圆半径与边心距相同、t为正五边形边长。

构造

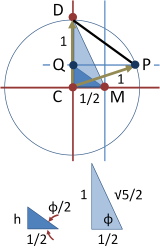
里士满提出了一个构造正五边形的方法 ，并且在克伦威尔的《多面体》中被近一步讨论。 。

右上的图显示了里士满绘制正五边形的方法。先利用单位圆决定五边形的半径。C为单位圆圆心，M是圆C半径的中点。D是位于垂直于MC的另外一条半径的圆周上。作角CMD的角平分线，令Q为角CMD的角平分线与CD的交点。作过Q平行于MC的直线，令之与圆C相交的交点为P，则DP为正五边形的边长。

这条边的长度可以利用圆下方的两个直角三角形DCM和QCM。利用勾股定理，较大的三角形斜边为 5 / 2 {\displaystyle \scriptstyle {\sqrt {5}}/2} 。小三角形其中一股 h 可由半角公式求得:

其中，角 ϕ 可由大三角形求得，其值为：

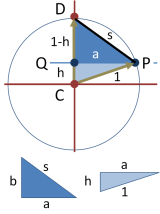
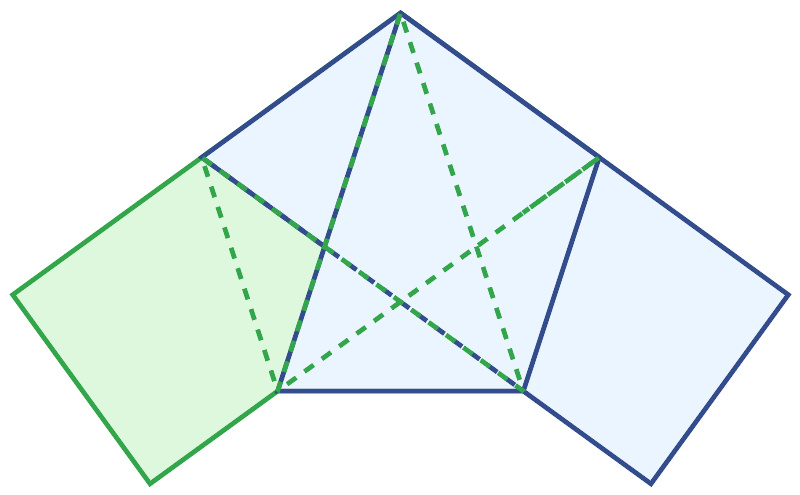
由此可得到在下图正五边形的边长的一些相关值。右侧三角形的边长a可借由再带一次勾股定理得：

欲求出五边形边长s可透过左侧的三角形，由勾股定理得：

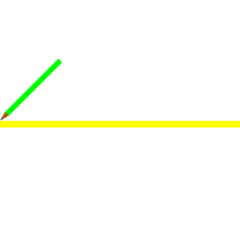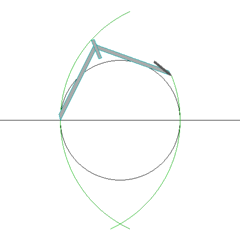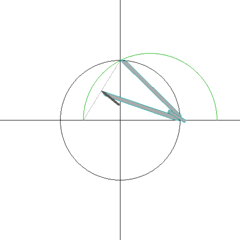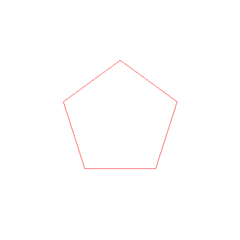
使用圆规与直尺建构出正五边形。

五边形边长s为：

得到了正确的结果 因此此种构造正五边形的方法是有效的。

约前300年，欧几里得在他的《几何原本》中描述了一个用直尺和圆规做出正五边形的过程。

物理方法

打一个反手结的长条纸张

正五边形可以借由尝试在一张长条纸张上打一个反手结，并将多出来的部分向后折来构造。这种折法被用在折纸星星上。

等边五边形

有两个直角的等边五边形

等边五边形是指五条边等长的五边形。等边五边形不一定是正五边形。由于其内角可以取自一个范围内的集合，而形成一个等边五边形的群，相比之下，正五边形由于其内角也固定了，因此是唯一的。

有两个直角的等边五边形由于外形与有屋顶的房屋形状非常相似，因此通常用作房子的符号。

五边形镶嵌

五边形镶嵌 是指用五边形镶嵌平面。截至2015年已知有15种凸五边形镶嵌平面 。

扭歪五边形

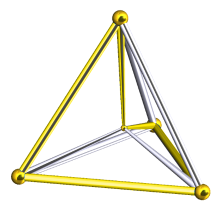
涂上黄色的边是一个扭歪五边形，位于四维正五胞体的施莱格尔图的透视投影。

扭歪五边形，又称不共面五边形，是指顶点并非完全共面的五边形。

皮特里多边形

一些高维度多胞体的 皮特里多边形 （ 英语 ： Petrie polygon ） 是扭歪五边形，例如四维正五胞体。

类五边形形

类五边形形是五边形在其他维度的类比。这些形状都具有H n 的可克斯特群 ，其中正五边形为H 2 ，阶数为10。

由五边形组成的多面体

有一些多面体由五边形构成，最常见的就是正二十面体，是一个由正五边形组成的正多面体。

参见

五边形镶嵌

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。