名称由来

误差函数来自测度论，后来与测量误差无关的其他领域也用到这一函数，但仍然使用误差函数这一名字。

误差函数与对正态分布积分的累积分布函数Φ Φ -->{\displaystyle \Phi }的关系为

性质

复平面上的图Integrand exp(−z)erf(z)

误差函数是奇函数：

对于任何复数z:

其中 z¯ ¯ -->{\displaystyle {\overline {z}}} 表示 z的复共轭。

复平面上，函数 ƒ = exp(−z) 和 ƒ = erf(z) 如图所示。粗绿线表示 Im(ƒ) = 0，粗红线表示 Im(ƒ) ƒ) > 0。细绿线表示 Im(ƒ) = constant，细红线表示 Re(ƒ) = constant0。

在实轴上， z → ∞时，erf(z) 趋于1，z → −∞时，erf(z) 趋于−1 。在虚轴上， erf(z) 趋于 ±i∞。

泰勒级数

误差函数是整函数，没有奇点（无穷远处除外），泰勒展开收敛。

误差函数泰勒级数：

对每个复数 z均成立。 上式可以用迭代形式表示：

误差函数的导数：

误差函数的不定积分为：

逆函数

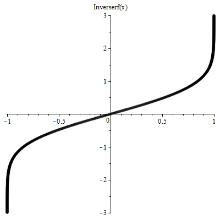
Inverse error function

逆误差函数 可由麦克劳林级数表示：

其中， c0 = 1 ，

即：

逆互补误差函数定义为：

渐近展开

互补误差函数的渐近展开，

其中 (2n – 1)!! 为双阶乘，x为实数，该级数对有限 x发散。对于N∈ ∈ -->N{\displaystyle N\in \mathbb {N} } ，有

其中余项用以大O符号表示为

余项的精确形式为：

对于比较大的 x, 只需渐近展开中开始的几项就可以得到 erfc(x)很好的近似值。(对于不太大的 x ，上文泰勒展开在0处可以快速收敛。)。

连分式展开

互补误差函数的连分式展开形式：

初等函数近似表达式

其中， a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108

其中， p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556

其中， a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638

其中， p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429

以上所有近似式适用范围是： x ≥ 0. 对于负的 x, 误差函数是奇函数这一性质得到误差函数的值， erf(x) = −erf(−x).

另有近似式：

其中，

该近似式在0或无穷的邻域非常准确，x整个定义域上，近似式最大误差小于0.00035，取 a ≈ 0.147 ，最大误差可减小到0.00012。

逆误差函数近似式:

数值近似

下式在整个定义域上，最大误差可低至 1.2⋅ ⋅ -->10− − -->7{\displaystyle 1.2\cdot 10^{-7}}：

其中，

与其他函数的关系

误差函数本质上与标准正态累积分布函数Φ Φ -->{\displaystyle \Phi }是等价的，

可整理为如下形式：

Φ Φ -->{\displaystyle \Phi }的逆函数为正态分位函数（英语：Quantile function），即概率单位（英语：Probit）函数，

误差函数为标准正态分布的尾概率Q函数（英语：Q-function）的关系为，

误差函数是米塔-列夫勒函数的特例，可以表示为合流超几何函数，

误差函数用正则Γ函数P和不完全Γ函数表示为

sgn⁡ ⁡ -->(x) {\displaystyle \scriptstyle \operatorname {sgn} (x)\ } 为符号函数.

广义误差函数

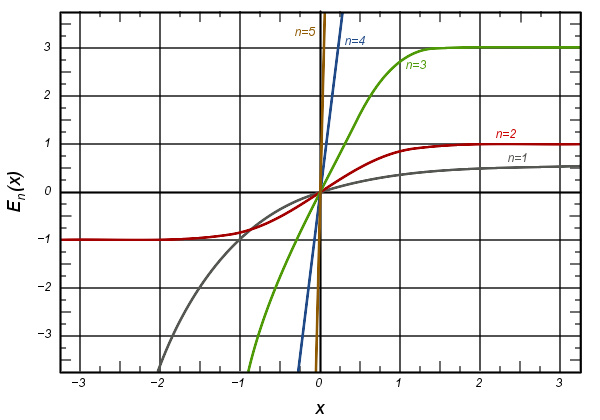
广义误差函数图像 En(x): 灰线: E1(x) = (1 − e)/π π -->{\displaystyle \scriptstyle {\sqrt {\pi }}} 红线: E2(x) = erf(x) 绿线: E3(x) 蓝线: E4(x) 金线: E5(x).

广义误差函数为：

其中，E0(x)为通过原点的直线， E0(x)=xeπ π -->{\displaystyle \scriptstyle E_{0}(x)={\frac {x}{e{\sqrt {\pi }}}}}。E2(x) 即为误差函数 erf(x)。

x > 0时，广义误差函数可以用Γ函数和 不完全Γ函数表示，

因此，误差函数可以用不完全Γ函数表示为：

互补误差函数的迭代积分

互补误差函数的迭代积分定义为：

可以展开成幂级数：

满足如下对称性质：

和

函数表

参见

古德温 - 斯塔顿积分

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。