由泰勒展开式的推导

首先假设要近似函数的各级导数都有良好的性质，依照泰勒定理，可以形成以下的泰勒展开式：

其中 n !表示是 n 的阶乘， R n ( x )为余数，表示泰勒多项式和原函数之间的差。可以推导函数 f 一阶导数的近似值：

设定x 0 =a，可得：

除以 h 可得：

求解f"(a)：

假设 R 1 ( x ) {\displaystyle R_{1}(x)} 相当小，因此可以将"f"的一阶导数近似为：

准确度及误差

近似解的误差定义为近似解及解析解之间的差值。有限差分法的两个误差来源分别是舍入误差及 截尾误差 （ 英语 ： truncation error ） （或称为离散化误差），前者是因为电脑计算小数时四舍五入造成的误差，后者则是计算机内数字位数限制造成的误差。

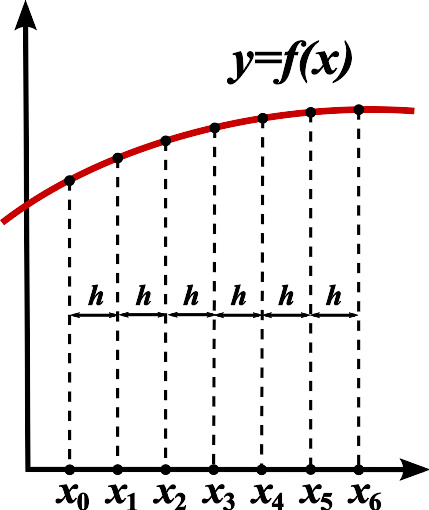
有限差分法是以在格点上函数的值为准

在运用有限差分法求解一问题（或是说找到问题的近似解）时，第一步需要将问题的定义域离散化。一般会将问题的定义域用均匀的网格分割（可参考右图）。因此有限差分法会制造一组导数的离散数值近似值。

一般会关注近似解的 局部截尾误差 （ 英语 ： local truncation error ） ，会用大O符号表示，局部截尾误差是指应用有限差分法一次后产生的误差，因此为 f ′ ( x i ) − − --> f i ′ {\displaystyle f"(x_{i})-f"_{i}} ，此时 f ′ ( x i ) {\displaystyle f"(x_{i})} 是实际值，而 f i ′ {\displaystyle f"_{i}} 为近似值。泰勒多项式的余数项有助于分析局部截尾误差。利用 f ( x 0 + h ) {\displaystyle f(x_{0}+h)} 泰勒多项式的余数项，也就是

可以找到局部截尾误差的主控项，例如用前项差分法计算一阶导数，已知 f ( x i ) = f ( x 0 + i h ) {\displaystyle f(x_{i})=f(x_{0}+ih)} ,

利用一些代数的处理，可得

注意到左边的量是有限差分法的近似，右边的量是待求解的量再加上一个余数，因此余数就是局部截尾误差。上述范例可以用下式表示：

在此例中，局部截尾误差和时间格点的大小成正比。

范例：常微分方程

例如考虑以下的常微分方程

利用数值方法中欧拉法求解，利用以下的有限差分式

来近似导数，并配合一些代数处理（等号两侧同乘以h，再加上u(x)），可得

最后的方程式即为有限差分方程，求解此方程则可得到原方程的近似解。

范例：热传导方程

考虑正规化的一维热传导方程式，为齐次的狄利克雷边界条件

对此问题求数值解的一种方式是用差分去近似所有的导数，可以将空间分割为 x 0 , . . . , x J {\displaystyle x_{0},...,x_{J}} ，将时间也分割为 t 0 , . . . . , t N {\displaystyle t_{0},....,t_{N}} 。假设在时间及空间都是均匀的网格切割，空间中两个连续位置的间隔为 h ，两个连续时间之间的间隔为 k 。点

表示 u ( x j , t n ) {\displaystyle u(x_{j},t_{n})} 的数值近似解。

显式方法

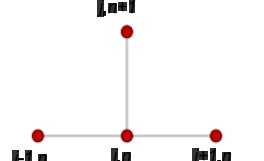
热传导方程最常用显式方法的 模版 （ 英语 ： Stencil (numerical analysis) ）

利用在时间 t n {\displaystyle t_{n}} 的前向差分，以及在位置 x j {\displaystyle x_{j}} 的二阶中央差分（ FTCS 格式 （ 英语 ： FTCS scheme ） ），可以得到以下的迭代方程：

这是用求解一维导热传导方程的 显式方法 （ 英语 ： Explicit and implicit methods ） 。

可以用以下的式子求解 u j n + 1 {\displaystyle u_{j}^{n+1}}

其中 r = k / h 2 . {\displaystyle r=k/h^{2}.}

因此配合此迭代关系式，已知在时间 n 的数值，可以求得在时间 n +1的数值。 u 0 n {\displaystyle u_{0}^{n}} 及 u J n {\displaystyle u_{J}^{n}} 的数值可以用边界条件代入，在此例中为0。

此显式方法在 r ≤ ≤ --> 1 / 2 {\displaystyle r\leq 1/2} 时，为数值稳定且收敛 。其数值误差和时间间隔成正比，和位置间隔的平方成正比：

隐式方法

隐式方法的模版

若使用时间 t n + 1 {\displaystyle t_{n+1}} 的后向差分，及位置 x j {\displaystyle x_{j}} 的二阶中央差分（BTCS 格式），可以得到以下的迭代方程：

这是用求解一维导热传导方程的 隐式方法 （ 英语 ： Explicit and implicit methods ） 。

在求解线性联立方程后可以得到 u j n + 1 {\displaystyle u_{j}^{n+1}} ：

此方法不论 r {\displaystyle r} 的大小，都数值稳定且收敛，但在计算量会较显式方法要大，因为每前进一个时间间隔，就需要求解一个联立的数值方程组。其数值误差和时间间隔成正比，和位置间隔的平方成正比：

克兰克－尼科尔森方法

若使用时间 t n + 1 / 2 {\displaystyle t_{n+1/2}} 的中间差分，及位置 x j {\displaystyle x_{j}} 的二阶中央差分（CTCS 格式），可以得到以下的迭代方程：

此公式为克兰克－尼科尔森方法（Crank-Nicolson方法）。

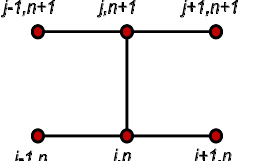
克兰克－尼科尔森方法的模版

在求解线性联立方程后可以得到 u j n + 1 {\displaystyle u_{j}^{n+1}} ：

此方法不论 r {\displaystyle r} 的大小，都数值稳定且收敛，但在计算量会较显式方法要大，因为每前进一个时间间隔，就需要求解一个联立的数值方程组。其数值误差和时间间隔的平方成正比，和位置间隔的平方成正比：

若时间刻度较小时，克兰克－尼科尔森方法是最精确的，而显式方法是最不精确的，而且可能会不稳定，但是是最容易计算的，其数值计算量也最少。若时间刻度较大时，隐式方法的效果最好。

相关条目

有限元分析

差分

时域有限差分

模版 (数值分析) （ 英语 ： Stencil (numerical analysis) ）

有限差分系数 （ 英语 ： Finite difference coefficient ）

五点Stencil （ 英语 ： Five-point stencil ）

Lax等价定理 （ 英语 ： Lax equivalence theorem ）

期权定价的有限差分法 （ 英语 ： finite difference methods for option pricing ）

参考资料

K.W. Morton and D.F. Mayers, Numerical Solution of Partial Differential Equations, An Introduction . Cambridge University Press, 2005.

Oliver Rübenkönig, The Finite Difference Method (FDM) - An introduction , (2006) Albert Ludwigs University of Freiburg

Autar Kaw and E. Eric Kalu, Numerical Methods with Applications , (2008)[1]

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。