构造

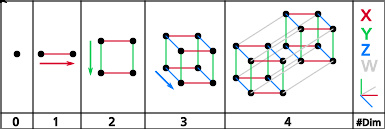
  一个展示如何从一个点构造出一个超正方体的图像

这个过程可以被推进到任意维度。这个扫出体积的过程可以被数学正式化为闵可夫斯基和： d 维超方形是 d 个互相垂直的单位长度线段的闵可夫斯基和，因此超方形是环带多面体的一个很好的例子。

超方体的1阶 骨架 （ 英语 ： Skeleton (topology) ） 是一个 超方形图 （ 英语 ： hypercube graph ） 。

顶点坐标

n 维的单位超方形是所有由直角坐标系 ( ± ± --> 1 2 , ± ± --> 1 2 , ⋯ ⋯ --> , ± ± --> 1 2 ) {\displaystyle \left(\pm {\frac {1}{2}},\pm {\frac {1}{2}},\cdots ,\pm {\frac {1}{2}}\right)} 的所有符号排列所对应的点组成的凸包。它的棱长为1，而它的 n 维超体积是1。

一个 n 维超方形有时也被表示为直角坐标 ( ± ± --> 1 , ± ± --> 1 , ⋯ ⋯ --> , ± ± --> 1 ) {\displaystyle (\pm 1,\pm 1,\cdots ,\pm 1)} 的所有符号排列所对应的点组成的凸包。这顶点坐标写法因为简便而经常被使用。它的棱长是2，而 n 维超体积是2 。

与其它多胞形家族的关系

超方形家族是少有的几个在任何维度都出现的正多胞形家族之一。

超方形 家族是三个正多胞形家族之一，被考克斯特标记为 γ n 。另外两个是超方形对偶 正轴形 家族，标记为 β n ，以及 正单纯形 家族，标记为 α n 。例外，还有第四个不由凸正多胞形而是正无穷胞形，即超空间密铺组成的家族超方形堆砌家族，标记为 δ n ，它们是超方形的超空间密铺。

另外一个与超方形相关的由一系列 半正多胞形 （ 英语 ： Uniform polytope ） 组成的半正家族是 半超方形 家族，它们可由交错地删除对应维度超方形的顶点并在切口上添加新的正单纯形面来构造，标记为 hγ n 。

元素

任何一个n-超方体（n>0）都是由低维的超方形元素组成的：它的(n-1)维表面（“维面”）是(n-1)维的超方形，它的(n-2)维边缘（“维脊”）是(n-2)维的超方形，它的(n-3)维元素（“维顶”）是(n-3)维的超方形…… n维的超方形有2n个维面（一维线段有两个端点；二维正方形有4条边或叫棱；三维立方体有6个面；四维超正方体有8个胞……）和 2 n {\displaystyle 2^{n}} 个顶点（例如，立方体有 2 3 {\displaystyle 2^{3}} 个顶点）。

一个简单的计算 n -超方体 "n-2" -面个数的公式是： 2 n 2 − − --> 2 n {\displaystyle 2n^{2}-2n}

n -超方形表面上 m 维超方形（0≤m≤n）的个数是：

例如，四维超正方体（n=4）包含了8个立方体（3-超方体）、24个正方形（2-超方体）、32个线段（1-超方体）和16个点（0-超方体）。

这个特性能够用组合学来证明。 2 n {\displaystyle 2^{n}} 个顶点中的每一个都决定了 n -超方体的一个 m {\displaystyle m} 维表面。我们有 ( n m ) {\displaystyle {\begin{smallmatrix}{n \choose m}\end{smallmatrix}}} 种方法来选择哪些线段（“边”）决定了这表面所在的空间。但是因为每个表面都有 2 m {\displaystyle 2^{m}} 个顶点，所以每个表面都被算了 2 m {\displaystyle 2^{m}} 次，因此我们需要将结果再除以这个数。由此我们得到了上述性质。

这个结果也能被递推关系式产生出来。

例如，将二维空间中的正方形向三维空间延伸，在4个顶点处延伸出4条棱，最后加上第二个正方形来形成一个立方体，我们能算出总共有 E 1 , 3 {\displaystyle E_{1,3}\!} = 12 条棱。

图像

一个 n维超正方体 能通过一个 扭曲正交投影 （ 英语 ： Petrie_polygon#The_hypercube_and_orthoplex_families ） 投影到 2n 边形中，这里展示出了从线段到十二维超正方体的12个超方形。

 旋转着的四维超正方体的透视投影

与 n -单纯形的关系

n -超方体的棱的图像等距同构于( n -1)-单纯形的 表面框架 （ 英语 ： Convex polytope#The_face_lattice ） 的哈斯图。这种特殊关系可以通过以适当的角度看 n -超方体使得相对的两个顶点处在图像的两个顶点，对应于( n -1)-单纯形自己和空集元素。每一个与最上方的顶点相连的顶点唯一的映射到( n -1)-单纯形的维面，再与之相连的顶点映射到单纯形的维脊，如此等等，并且与最下方的顶点相连的顶点映射到单纯形的棱。

这个特殊关系可以被用来高效地产生( n-1 )-单纯形的表面框架，毕竟可用于计算所有多胞形表面框架的一般方法在计算上比较困难。

另见

超正八面体对称群 （ 英语 ： Hyperoctahedral group ） ，超方形的对称性

超球面

单纯形

超立方体互联网络，网络工程学

参考

Bowen, J. P.Hypercubes. Practical Computing. April 1982, 5 (4): 97–99.

Coxeter, H. S. M. 《正多胞形》 3rd. Dover. 1973: 123. ISBN 0-486-61480-8. p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n dimensions ( n ≥ 5)

Hill, Frederick J.; Gerald R. Peterson. Introduction to Switching Theory and Logical Design: Second Edition. NY: John Wiley & Sons. ISBN 0-471-39882-9. Cf Chapter 7.1 "Cubical Representation of Boolean Functions" wherein the notion of "hypercube" is introduced as a means of demonstrating a distance-1 code (Gray code) as the vertices of a hypercube, and then the hypercube with its vertices so labelled is squashed into two dimensions to form either a Veitch diagram or Karnaugh map.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。